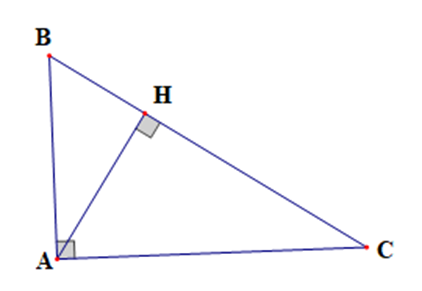
a) AB = 6 cm, BC = 10 cm. Tính AC, BH, HC, AH.
• Vì tam giác ABC vuông tại A nên BC2 = AB2 + AC2 (định lí Pytago)
Suy ra \(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\) (cm)
• Xét DABC vuông tại A có AH là đường cao nên ta có:
AB2 = BH.BC, suy ra \(BH = \frac{{A{B^2}}}{{BC}} = \frac{{{6^2}}}{{10}} = 3,6\left( {cm} \right)\).
AC2 = CH.BC, suy ra \(CH = \frac{{A{C^2}}}{{BC}} = \frac{{{8^2}}}{{10}} = 6,4\left( {cm} \right)\).
AH . BC = AB . AC, suy ra \(AH = \frac{{AB.AC}}{{BC}} = \frac{{6.8}}{{10}} = 4,8\left( {cm} \right)\)
b) BH = 1 cm, AH = 2 cm. Tính HC, AC, BA, BC.
• Vì tam giác ABC vuông tại A có AH là đường cao nên:
AH2 = BH.CH, suy ra \[CH = \frac{{A{H^2}}}{{BH}} = \frac{{{2^2}}}{1} = 4\left( {cm} \right)\].
• Vì DACH vuông tại H nên AC2 = AH2 + CH2 (định lí Pytago)
Suy ra \(AC = \sqrt {{2^2} + {4^2}} = 2\sqrt 5 \left( {cm} \right)\).
• Vì DABH vuông tại H nên BA2 = HB2 + AH2 (định lí Pytago)
Suy ra \(AB = \sqrt {B{H^2} + A{H^2}} = \sqrt {{1^2} + {2^2}} = \sqrt 5 \) (cm)
• Xét DABC vuông tại A có AH là đường cao nên AB2 = BH . BC
Suy ra \(BC = \frac{{A{B^2}}}{{BH}} = \frac{{{{\left( {\sqrt 5 } \right)}^2}}}{1} = 5\left( {cm} \right)\).
c) BH = 4 cm, HC = 9 cm. Tính BC, AB, AH, AC.
• Ta có BC = BH + CH = 4 + 9 = 13 (cm).
• Xét DABC vuông tại A có AH là đường cao nên AB2 = BH . BC (hệ thức lượng trong tam giác vuông)
Suy ra \(AB = \sqrt {BH.BC} = \sqrt {4.13} = 2\sqrt {13} \left( {cm} \right)\)
• Xét DABC vuông tại A có AH là đường cao nên AH2 = BH.CH (hệ thức lượng trong tam giác vuông)
Suy ra \(AH = \sqrt {BH.CH} = \sqrt {4.9} = 6\left( {cm} \right)\).
• Vì DABC vuông tại A nên BC2 = AB2 + AC2 (định lí Pytago)
Suy ra \(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{13}^2} - {{\left( {2\sqrt {13} } \right)}^2}} = 3\sqrt {13} \) (cm).
d) BH = 9 cm, AC = 20 cm. Tính HC, AH, AB, BC.
Xét DABC vuông tại A có AH là đường cao nên
• AC2 = CH . BC (hệ thức lượng trong tam giác vuông)
Û 202 = CH.(CH + BH)
Û 400 = CH.(CH + 9)
Û 400 = CH2 + 9CH
Û CH2 + 9CH – 400 = 0
Û CH = 16 cm (do CH > 0)
• AH2 = BH.CH = 9.16 = 144, suy ra AH = 12 (cm).
Xét DABH vuông tại H có AB2 = AH2 + BH2 (định lí Pytago)
Suy ra \(AB = \sqrt {A{H^2} + B{H^2}} = \sqrt {{{12}^2} + {9^2}} = \sqrt {225} = 15\left( {cm} \right)\)
Xét DABC vuông tại A nên BC2 = AB2 + AC2 (định lí Pytago)
Suy ra \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{{15}^2} + {{20}^2}} = 25\) (cm)