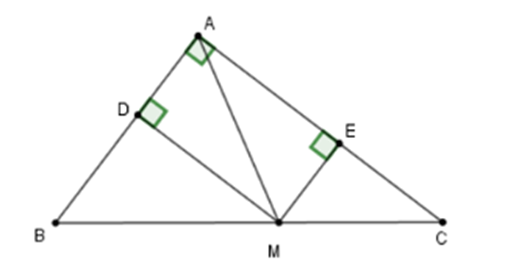
Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất?

A. M là hình chiếu của A trên BC.

B. M là trung điểm của BC.

C. M trùng B.

D. Đáp án khác.

Đáp án đúng là: A

Xét tứ giác ADME có

\(\widehat {DA{\rm{E}}} = \widehat {A{\rm{E}}M} = \widehat {A{\rm{D}}M} = 90^\circ \)

Suy ra ADME là hình chữ nhật

Do đó AM = DE

Để DE nhỏ nhất thì AM nhỏ nhất

Khi đó M là hình chiếu của A trên BC

Vậy ta chọn đáp án A.