Lời giải
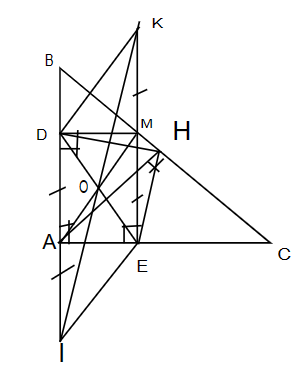
a) Vì MD ⊥ AB nên \(\widehat {M{\rm{D}}A} = 90^\circ \)
ME ⊥ AC nên \(\widehat {MEA} = 90^\circ \)
Vì tam giác ABC vuông tại A nên \(\widehat {BAC} = 90^\circ \)
Xét tứ giác ADME có \(\widehat {M{\rm{D}}A} = 90^\circ \), \(\widehat {MEA} = 90^\circ \), \(\widehat {DAE} = 90^\circ \)
Suy ra ADME là hình chữ nhật
Mà AM, DE là 2 đường chéo
Suy ra AD = ME, AM = DE, AM cắt DE tại trung điểm của mỗi đoạn
Vậy AM = DE.
b) Gọi O là giao điểm của AM và DE
Nên ta có O là trung điểm của AM, DE (chứng minh câu a) (1)
Vì I là điểm đối xứng của D qua A và K là điểm đối xứng của E qua M
Nên \[IA = AD = \frac{1}{2}DI,\,\,\,KM = EM = \frac{1}{2}KE\]
Mà AD = ME (chứng minh câu a)
Suy ra DI = KE
Ta có DI ⊥ AC, KE ⊥ AC
Suy ra DI // KE (quan hệ từ vuông góc đến song song)
Xét tứ giác DKEI có DI // KE và DI = KE (chứng minh trên)
Suy ra DKEI là hình bình hành
Suy ra DE cắt KI tại trung điểm của mỗi đường
Mà O là trung điểm của DE
Do đó O là trung điểm của KI (2)
Từ (1) và (2) suy ra các đoạn thẳng IK, DE, AM đồng quy tại trung điểm O của mỗi đoạn
c) Vì tam giác AHM vuông tại H, HO là đường trung tuyến
nên \[HO = \frac{1}{2}AM\]
Mà AM = DE
Suy ra HO = \(\frac{1}{2}\)DE
Xét tam giác DHE có \[HO = \frac{1}{2}DE\], HO là trung tuyến
Suy ra tam giác DHE vuông tại H
Do đó \(\widehat {DHE} = 90^\circ \)
d) Để hình bình hành DIKE là hình thoi
Thì EK = EI
Mà EK = 2EM, EI = AM
Suy ra AM = 2EM
Xét tam giác AEM vuông tại E có AM = 2EM
Suy ra \(\widehat {MAE} = 30^\circ \)
Vậy lấy M thuộc BC sao cho \(\widehat {MAC} = 30^\circ \) thì tứ giác DIEK là hình thoi.

