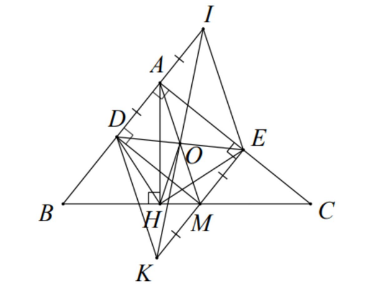
Cho tam giác ABC vuông tại A điểm M thuộc cạnh BC từ M vẽ các đường thẳng vuông góc

Đề bài: Cho $\Delta ABC$ vuông tại A điểm M thuộc cạnh BC từ M vẽ các đường thẳng vuông góc với AB ở D vuông góc với AC ở E

a) cm AM = BE.

b) gọi l là điểm đx của D qua A và K là điểm đx của E qua M cm IK, DE, AM đồng quy hai trung điểm O của mỗi đoạn.

c) gọi AH là đường cao của tính số đo $\widehat{DHE}$ .

Trả lời

Hướng dẫn giải:

a) Xét tứ giác ADME có $\widehat{\text{DAE}}\text{ =}\widehat{\text{ ADM}}\text{ = }\widehat{\text{AEM}}{\text{ = 90}}^{\text{o}}$

$\Rightarrow$ADME là hình chữ nhật

$\Rightarrow$AM= DE

b) Gọi O là giao điểm của AM và DE $\Rightarrow$  OA = OM = OD = OE (2)

Do ADME là hình chữ nhật $\Rightarrow$  DA = ME

$\Rightarrow$ 2DA = 2ME hay DA + AI = EM + MK (vì DA = AI; ME = MK)

$\Rightarrow$ DI = EK

Xét tứ giác DIEK có DI = EK (cmt)

     DI // EK (vì CEDM là HCN)

$\Rightarrow$ DKEI là hình bình hành

Do O là trung điểm của DE $\Rightarrow$  KI đi qua O

$\Rightarrow$ DE cắt IK tại O và OD = OE;  OK = OI (1) 

Từ (1) và (2) $\Rightarrow$  DE; AM; IK đồng quy tại trung điểm O của mỗi đường

c) Xét AHM vuông tại H có O là trung điểm của AM, khi đó HO là đường trung tuyến ứng với cạnh huyền AM. Suy ra $\text{HO = }\frac{\text{1}}{\text{2}}\text{ . AM}$

Mặt khác, AM = DE.

 $\Rightarrow \text{HO = }\frac{\text{1}}{\text{2}}\text{ . DE}$

Xét DHO có đường trung tuyến  $\text{HO = }\frac{\text{1}}{\text{2}}\text{ . DE}$

$\Rightarrow$ DHE vuông tại H  $\Rightarrow \widehat{\text{DHE}}{\text{ = 90}}^{\text{o}}$