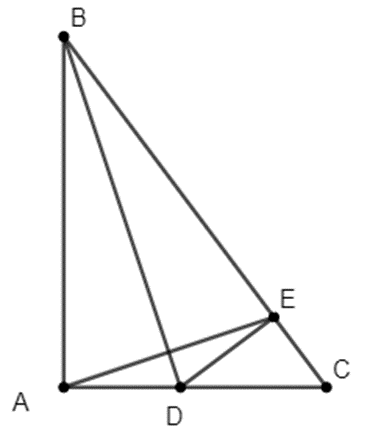
Cho tam giác ABC vuông tại A có \(\widehat B = 60^\circ \).
a) Tính số đo góc C.
b) Trên BC lấy E sao cho BE = BA, tia phân giác của góc B cắt AC tại D. Chứng minh: DE = AD.
a) Xét ∆BAC có: \(\widehat A = 90^\circ \)
\( \Rightarrow \widehat B + \widehat C = 90^\circ \)
\( \Leftrightarrow 60^\circ + \widehat C = 90^\circ \Leftrightarrow \widehat C = 30^\circ \)
b) Xét ∆ABE có
BD là đường phân giác của ∆ABE.
Mặt khác ∆ABE cân tại B nên suy ra BD cũng là đường trung trực của ∆ABE.
Theo tính chất của đường trung trực ta có: DA = DE.