Cho tam giác ABC vuông tại A có đường cao AH. Kẻ HM vuông góc với AB tại M. Chứng minh rằng ΔAMH ᔕ ΔAHB

Bài 7 trang 76 Toán 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Kẻ HM vuông góc với AB tại M.

a) Chứng minh rằng ΔAMH ᔕ ΔAHB.

b) Kẻ HN vuông góc với AC tại N. Chứng minh rằng AM.AB = AN.AC.

c) Chứng minh rằng ΔANM ᔕ ΔABC.

d) Cho biết AB = 9 cm, AC = 12 cm. Tính diện tích tam giác AMH.

Trả lời

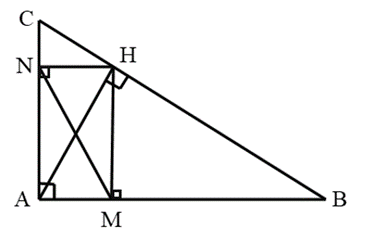
a) Xét hai tam giác vuông AMH và AHB có:  $\hat{\mathrm{A}}$ chung

Suy ra ΔAMH ᔕ ΔAHB (g.g)

b) ΔAMH ᔕ ΔAHB nên $\frac{\mathrm{AM}}{\mathrm{AH}}=\frac{\mathrm{AH}}{\mathrm{AB}}$ hay AM.AB = AH² (1)

Xét hai tam giác vuông ANH và AHC có: $\hat{\mathrm{A}}$  chung

Suy ra ΔANH ᔕ ΔAHC (g.g) nên $\frac{\mathrm{AN}}{\mathrm{AH}}=\frac{\mathrm{AH}}{\mathrm{AC}}$  hay AN.AC = AH² (2)

Từ (1) và (2) suy ra AM.AB = AN.AC (đpcm).

c) Ta có AM.AB = AN.AC, do đó  $\frac{\mathrm{AN}}{\mathrm{AB}}=\frac{\mathrm{AM}}{\mathrm{AC}}$.

Xét hai tam giác vuông AMN và ABC có:

$\frac{\mathrm{AN}}{\mathrm{AB}}=\frac{\mathrm{AM}}{\mathrm{AC}}$ (chứng minh trên)

Do đó ΔANM ᔕ ΔABC (c.g.c)

d) Áp dụng định lí Pythagore vào tam giác ABC, ta có: 

BC² = AB² + AC² = 9² + 12² = 225.

Suy ra BC = 15 cm.

Xét hai tam giác vuông ABC và HBA có $\hat{\mathrm{B}}$ chung

Do đó ΔABC ᔕ ΔHBA (g.g).

Suy ra $\frac{\mathrm{AC}}{\mathrm{AH}}=\frac{\mathrm{BC}}{\mathrm{AB}}$ (các cặp cạnh tương ứng).

Khi đó AH.BC = AB.AC hay AH.15 = 9.12.

Suy ra AH = 7,2 cm.

• Từ (1): AM.AB = AH² nên $\mathrm{AM}=\frac{{\mathrm{AH}}^2}{\mathrm{AB}}=\frac{7,2^2}{9}=5,76\left(\mathrm{cm}\right)$

• Từ (2): AN.AC = AH² nên $\mathrm{AN}=\frac{{\mathrm{AH}}^2}{\mathrm{AC}}=\frac{7,2^2}{12}=4,32\left(\mathrm{cm}\right)$

Diện tích tam giác AMN là: 

$\frac{1}{2}.5,76.4,32=12,4416\left({\mathrm{cm}}^2\right)$.

Vậy diện tích tam giác AMN là 12,4416 cm².

Xem thêm các bài giải SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Hai tam giác đồng dạng

Bài 2: Các trường hợp đồng dạng của hai tam giác

Bài 3: Các trường hợp đồng dạng của hai tam giác vuông

Bài 4: Hai hình đồng dạng

Bài tập cuối chương 8

Bài 1: Mô tả xác suất bằng tỉ số