Lời giải
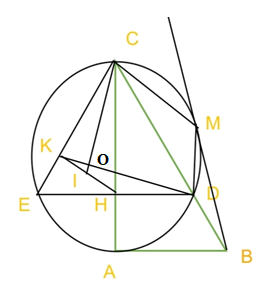
a) Xét tam giác ABC vuông tại A có \(\sin \widehat {ACB} = \frac{{AC}}{{BC}}\)
Suy ra \(\sin 30^\circ = \frac{6}{{BC}}\)
Suy ra BC = 6 . 2 = 12 (cm)
b) Xét đường tròn đường kính AC có DE ⊥ AC
Suy ra AC đi qua trung điểm của DE, H là trung điểm của DE
Xét tam giác ECD có CH vừa là đường cao vừa là đường trung tuyến
Suy ra tam giác ECD cân tại C và CH là tia phân giác của \(\widehat {EC{\rm{D}}}\)
Do đó \(\widehat {EC{\rm{D}}} = 2\widehat {ACB} = 2.30 = 60^\circ \)
Suy ra tam giác ECD đều
Vậy tam giác ECD đều
c) Xét đường tròn đường kính AC có \(\widehat {{\rm{BMD}}},\widehat {{\rm{MCD}}}\) là hai góc chắn cung MD
Suy ra \(\widehat {{\rm{BMD}}} = \widehat {{\rm{MCD}}}\)
Xét tam giác MDB và tam giác CMB có
\(\widehat {{\rm{BMD}}} = \widehat {{\rm{MCD}}}\) (chứng minh trên)
\(\widehat {{\rm{MBC}}}\) là góc chung
Suy ra tam giác BDM đồng dạng với tam giác BMC
Vậy tam giác BDM đồng dạng với tam giác BMC
d) Vì tam giác EHK vuông tại K
Nên \(\widehat {KEH} + \widehat {KHE} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Mà \(\widehat {KHC} + \widehat {KHE} = \widehat {CHE} = 90^\circ \)
Suy ra \(\widehat {KEH} = \widehat {KHC}\)
Xét tam giác KEH và tam giác KHC có
\(\widehat {KEH} = \widehat {KHC}\) (chứng minh trên)
\(\widehat {EKH} = \widehat {HKC}\left( { = 90^\circ } \right)\)
Do đó (g.g)
Suy ra \(\frac{{KH}}{{HC}} = \frac{{EK}}{{EH}}\)
Suy ra \(\frac{{KH}}{{2HC}} = \frac{{EK}}{{2EH}}\)
Do đó \(\frac{{IH}}{{HC}} = \frac{{EK}}{{DE}}\)
Xét tam giác IHC và tam giác KED có
\(\frac{{IH}}{{HC}} = \frac{{EK}}{{DE}}\) (chứng minh trên)
\(\widehat {KED} = \widehat {IHC}\)(chứng minh trên)
Do đó (c.g.c)
Suy ra \(\widehat {KDE} = \widehat {ICH}\) (hai góc tương ứng)
Vì tam giác CHD vuông tại H
Nên \(\widehat {HC{\rm{D}}} + \widehat {HDC} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
\( \Leftrightarrow \widehat {HC{\rm{D}}} + \widehat {HDK} + \widehat {KDC} = 90^\circ \)
\( \Leftrightarrow \widehat {HC{\rm{D}}} + \widehat {ICH} + \widehat {KDC} = 90^\circ \)
\( \Leftrightarrow \widehat {IC{\rm{D}}} + \widehat {KDC} = 90^\circ \)
Gọi giao điểm của CI và KD là O
Xét tam giác OCD có \(\widehat {OC{\rm{D}}} + \widehat {ODC} + \widehat {DOC} = 180^\circ \)
Hay \(\widehat {DOC} = 180^\circ - 90^\circ = 90^\circ \)
Suy ra CI ⊥ DK
Vậy CI ⊥ DK.

