Cho tam giác ABC vuông tại A có AB < AC. Vẽ AD là tia phân giác của góc BAC (D ∈ BC). Trên AC lấy điểm E sao cho AE = AB

Bài 106 trang 99 SBT Toán 7 Tập 2: Cho tam giác ABC vuông tại A có AB < AC. Vẽ AD là tia phân giác của góc BAC (D ∈ BC). Trên AC lấy điểm E sao cho AE = AB.

a) Chứng minh $\widehat{ABD}=\widehat{AED}$.

b) Tia ED cắt AB tại F. Chứng minh AC = AF.

c) Gọi G là trung điểm của DF; AD cắt CF tại H và cắt CG tại I. Chứng minh DI = 2IH.

Trả lời

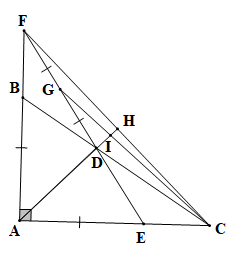
a) Xét $∆$ABD và $∆$EAD có:

AB = AE (giả thiết),

$\widehat{BAD}=\widehat{EAD}$ (do AD là tia phân giác của góc BAC)

AD là cạnh chung

Suy ra ∆ABD = ∆AED (c.g.c)

Do đó $\widehat{ABD}=\widehat{AED}$ (hai góc tương ứng)

Vậy $\widehat{ABD}=\widehat{AED}$.

b) Xét $∆$ABC và $∆$AEF có:

$\widehat{FAC}$ là góc chung,

AB = AE (giả thiết),

$\widehat{ABC}=\widehat{AEF}$ (Do $\widehat{ABD}=\widehat{AED}$)

Suy ra ∆ABC = ∆AEF (g.c.g)

Do đó AC = AF (hai cạnh tương ứng)

Vậy AC = AF.

c) Xét ∆AHF và DAHC có:

AH là cạnh chung,

$\widehat{FAH}=\widehat{CAH}$ (do AD là tia phân giác của góc BAC),

AF = AC (chứng minh câu b)

Do đó ∆AHF = $∆$AHC (c.g.c)

Suy ra HF = HC (hai cạnh tương ứng).

Khi đó H là trung điểm của FC nên DH là đường trung tuyến xuất phát từ đỉnh D của tam giác DFC.

Xét tam giác DFC có CG và DH là hai đường trung tuyến, CG và DH cắt nhau tại I

Suy ra I là trọng tâm của tam giác DFC.

Do đó IH = $\frac{1}{2}$ID (tính chất trọng tâm của tam giác)

Hay DI = 2IH.

Vậy DI = 2IH.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 9. Đường trung trực của một đoạn thẳng

Bài 10. Tính chất ba đường trung tuyến của tam giác

Bài 11. Tính chất ba đường phân giác của tam giác

Bài 12. Tính chất ba đường trung trực của tam giác

Bài 13. Tính chất ba đường cao của tam giác

Bài tập cuối chương 7