Cho tam giác ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng d

Đề bài: Cho tam giác ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng d (B, C nằm cùng phía đối với d). Kẻ BM và CN vuông góc với d. Chứng minh rằng:

a) ∆BAM = ∆CAN.

b) MN = BM + CN.

Trả lời

Hướng dẫn giải:

a) Xét tam giác ACN vuông tại N

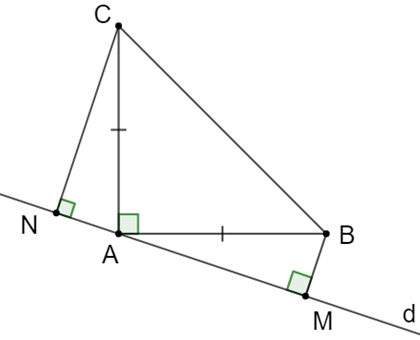
a) Xét tam giác ACN vuông tại N

$\Rightarrow \widehat{NCA}+\widehat{NAC}=90°$ (1)

Mà $\widehat{NAC}+\widehat{MAB}=180°-\widehat{BAC}=90°$  (2)

Từ (1) và (2) suy ra $\widehat{NCA}=\widehat{MAB}$  (hai góc cùng phụ với $\widehat{NAC}$)

Xét ∆NCA và ∆MAB vuông tại N và M có:

$\widehat{NCA}=\widehat{MAB}$ (cmt)

AC = BA (gt)

Þ ∆NCA = ∆MAB (cạnh huyền – góc nhọn)

Vậy ∆BAM = ∆CAN (đpcm).

b) ∆NCA = ∆MAB Þ BM = AN và CN = AM (các cặp cạnh tương ứng bằng nhau)

Þ MN = MA + AN = CN + BM

Vậy MN = BM + CN (đpcm)