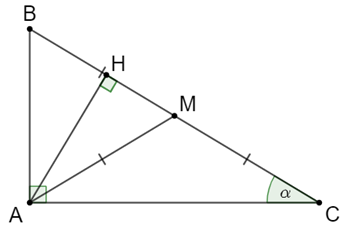
Cho tam giác ABC vuông tại A, AB < AC, góc C = a < 45°, đường trung tuyến AM, đường cao AH, MA = MB = MC. Chứng minh: sin 2alpha  = 2sin alpha .cos alpha

Trả lời

Lời giải

Ta có:

\(\sin 2\alpha = \sin \left( {2\widehat {ACB}} \right) = \sin \left( {\widehat {MCA} + \widehat {MAC}} \right)\)

\( = \sin \left( {\widehat {AMH}} \right) = \frac{{AH}}{{AM}} = \frac{{2AH}}{{BC}}\)

\( = 2.\frac{{AH}}{{AC}}.\frac{{AC}}{{BC}} = 2\sin \alpha .\cos \alpha \)