Lời giải
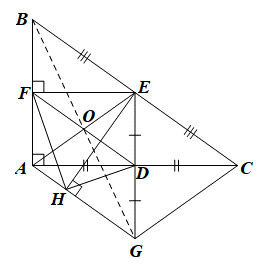
a) Xét DABC có D, E lần lượt là trung điểm của AC và BC nên DE là đường trung bình của tam giác
Do đó DE // AB hay DE // AF.
Ta có AB ⊥ AC và DE // AB nên DE ⊥ AC hay \(\widehat {ADE} = 90^\circ \).
Xét tứ giác ADEF có: \(\widehat {FAD} = \widehat {ADE} = \widehat {AFE} = 90^\circ \)
Do đó ADEF là hình chữ nhật (dấu hiệu nhận biết).
b) Tứ giác AECG có hai đường chéo AC và GE cắt nhau tại trung điểm D của mỗi đường nên là hình bình hành.
Lại có hai đường chéo EG ⊥ AC (do DE ⊥ AC)
Do đó AECG là hình thoi.
c) Do ADEF là hình chữ nhật nên hai đường chéo AE và DF cắt nhau tại trung điểm của mỗi đường, hay O là trung điểm của AE.
Do AECG là hình thoi nên EC // AG và EC = AG
Lại có BE = EC (do E là trung điểm của BC) nên BE = AG.
Xét tứ giác ABEG có BE // AG (do EC // AG) và BE = AG
Do đó ABEG là hình bình hành
Suy ra hai đường chéo AE và BG cắt nhau tại trung điểm của mỗi đường
Mà O là trung điểm của AE nên O là trung điểm của BG
Do đó ba điểm B, O, G thẳng hàng.
d) Do ADEF là hình chữ nhật nên AF = DE.
Mà DE = DG nên DG = AF.
Xét tứ giác AFDG có: DG = AF và DG // AF (do DE // AB)
Do đó AFDG là hình bình hành.
Suy ra AG // DF
Lại có EH ⊥ AG nên EH ⊥ DF
Xét DEHG vuông tại H có HD là đường trung tuyến ứng với cạnh huyền
Nên HD = ED = \(\frac{1}{2}EG\).
Khi đó DEDH là tam giác cân tại D
Suy ra đường cao DF của tam giác đồng thời là đường phân giác.
Hay \(\widehat {EDF} = \widehat {HDF}\).
Xét DEDF và DHDF có:
DF là cạnh chung;
\(\widehat {EDF} = \widehat {HDF}\) (chứng minh trên);
ED = HD (chứng minh trên)
Do đó DEDF = DHDF (c.g.c)
Suy ra \(\widehat {FED} = \widehat {FHD}\) (hai góc tương ứng)
Mà \(\widehat {FED} = 90^\circ \) (do ADEF là hình chữ nhật)
Do đó \(\widehat {FHD} = 90^\circ \), nên tam giác DHF vuông tại H.

