Cho tam giác ABC vuông ở A và hình vuông BCDE. Chứng minh rằng: AB + AC ≤ CE
Câu 13: Cho tam giác ABC vuông ở A và hình vuông BCDE. Chứng minh rằng:
AB + AC ≤ CE.
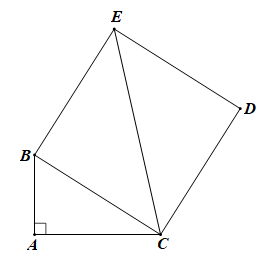
Áp dụng định lí Pythagore cho tam giác vuông ABC ta có: AB2 + AC2 = BC2.
Khi đó (AB + AC)2 = AB2 + AC2 + 2.AB.AC = BC2 + 2.AB.AC
Áp dụng bất đẳng thức Cosi ta có:
2.AB.AC ≤ AB2 + AC2 = BC2
⇒ (AB + AC)2 ≤ BC2 + BC2
Mà BC = BE (do BCDE là hình vuông) và BC2 + BE2 = CE2 (định lí Pythagore cho tam giác vuông BCE)
⇒ (AB + AC)2 ≤ BC2 + BE2 = CE2
⇒ AB + AC ≤ CE
Dấu “=” xảy ra khi AB = AC ⇔ ∆ABC vuông cân ở A.