Cho $\Delta ABC$ vuông cân tại A, tia phân giác của góc B và góc C cắt AC và AB lần lượt tại E và D.

a) Chứng minh BE = CD, AD = AE.

b) Gọi I là giao điểm của BE và CD, AI cắt BC tại M. Chứng minh $\Delta MAC$ vuông cân.

c) Từ A và D vẽ các đường thẳng vuông góc với BE. Các đường này cắt BC tại K và H. Chứng minh HK = KC.

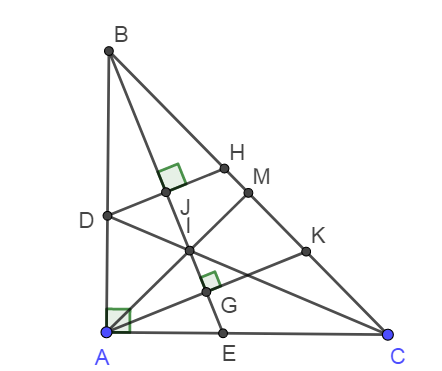
a) Do tam giác ABC vuông cân nên $\widehat{\text{ABC}}\text{ =}\widehat{\text{ ACB}}\Rightarrow \widehat{\text{ABE}}\text{ = }\widehat{\text{ACD}}$

Xét tam giác vuông ABE và tam giác vuông ACD có:

AB = AC (gt)

$\widehat{\text{ABE}}\text{ = }\widehat{\text{ACD}}$

$\Rightarrow \text{ΔABE = ΔACD}$ (Cạnh góc vuông - góc nhọn kề)

$\Rightarrow$ BE = CD; AE = AD

b) I là giao điểm của hai tia phân giác góc B và góc C của $\Delta ABC$nên AI cũng là phân giác góc A.

Do $\Delta ABC$ cân tại A nên AI là phân giác đồng thời là đường cao và trung tuyến.

Vậy thì $\widehat{\text{AMC}}{\text{ = 90}}^{\text{o}}\text{; BM = MC = AM}$

Từ đó suy ra $\Delta AMC$ vuông cân tại M.

c) Gọi giao điểm của DH, AK với BE lần lượt là J và G.

Do DH và AK cùng vuông góc với BE nên ta có

$\text{ΔBDJ = ΔBHJ; ΔBAG = ΔBKG}\Rightarrow \text{BD = BH; BA = BK}$

$\Rightarrow HK=AD$

Mà AD = AE nên HK = AE.    (1)

Do $∆BAK$ cân tại B, có ${}^{\text{o}}\Rightarrow \widehat{\text{BAK}}\text{ = }\frac{{\text{180}}^{\text{o}}{\text{ - 45}}^{\text{o}}}{\text{2}}{\text{ = 67,5}}^{\text{o}}$

$\Rightarrow \widehat{\text{GAE}}{\text{ = 90}}^{\text{o}}{\text{ - 67,5}}^{\text{o}}{\text{ = 22,5}}^{\text{o}}\text{ = }\frac{\widehat{\text{IAE}}}{\text{2}}$

Suy ra AG là phân giác góc IAE.

Từ đó ta có $\widehat{\text{KAC}}\text{ = }\widehat{\text{ICA}}\left({\text{ = 22,5}}^{\text{o}}\right)$

$\Rightarrow \text{ΔAKC = ΔCIA}\left(\text{g - c - g}\right)\Rightarrow \text{KC = IA}$

Lại có $∆AIE$có AG là phân giác đồng thời đường cao nên nó là tam giác cân, hay AI = AE. Suy ra KC = AE (2)

Từ (1) và (2) suy ra HK = KC.