Cho tam giác ABC vuông cân đỉnh A. Qua A kẻ đường thẳng d cắt BC. Vẽ BM, CN cùng vuông góc với d. Chứng minh: ∆BAM = ∆CAN.

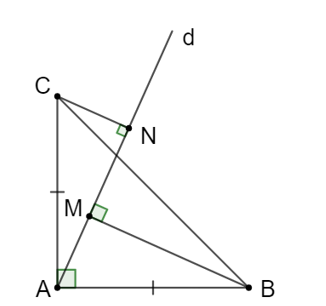
Xét tam giác ACN vuông tại N

$\Rightarrow \widehat{NCA}+\widehat{NAC}=90°$ (1)

Mà $\widehat{NAC}+\widehat{MAB}=\widehat{BAC}=90°$  (2)

Từ (1) và (2) suy ra $\widehat{NCA}=\widehat{MAB}$ (hai góc cùng phụ với $\widehat{NAC}$

Xét ∆NCA và ∆MAB vuông tại N và M có:

$\widehat{NCA}=\widehat{MAB}$ (cmt)

AC = BA (hai cạnh góc vuông của tam giác vuông cân)

Do đó ∆NCA = ∆MAB (cạnh huyền – góc nhọn)

Vậy ∆BAM = ∆CAN (đpcm).