Cho tam giác ABC vuông cân đỉnh A. Qua A kẻ đường thẳng d cắt BC. Vẽ BM, CN cùng vuông góc với d. Chứng minh ∆BAM = ∆ACN.
Cho tam giác ABC vuông cân đỉnh A. Qua A kẻ đường thẳng d cắt BC. Vẽ BM, CN cùng vuông góc với d. Chứng minh ∆BAM = ∆ACN.
Lời giải
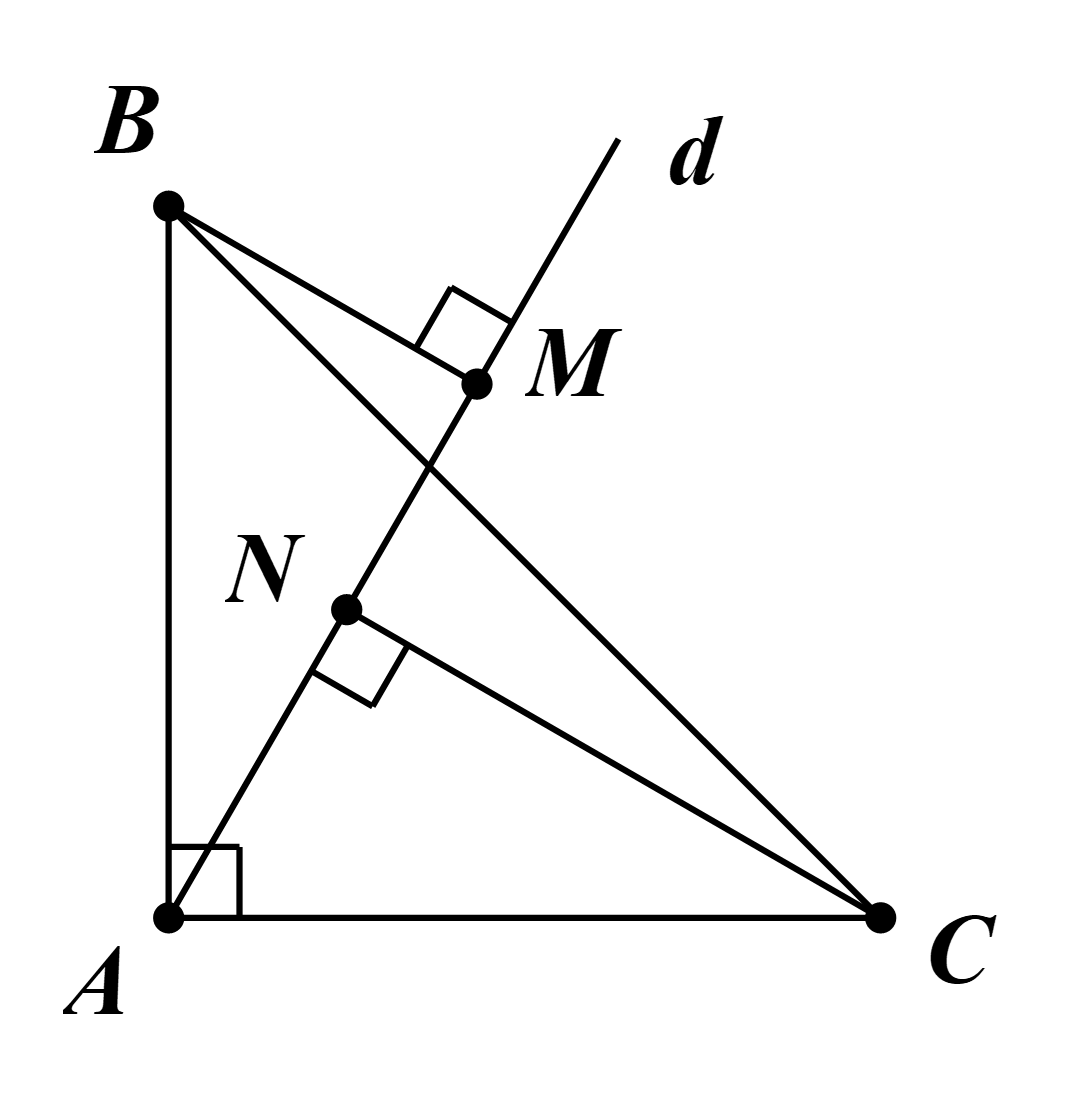
Xét ∆BAM và ∆ACN, có:
\[\widehat {BMA} = \widehat {ANC} = 90^\circ \];
AB = AC (do tam giác ABC vuông cân đỉnh A);
\(\widehat {BAM} = \widehat {ACN}\) (cùng phụ với \(\widehat {NAC}\)).
Do đó ∆BAM = ∆ACN (cạnh huyền – góc nhọn).