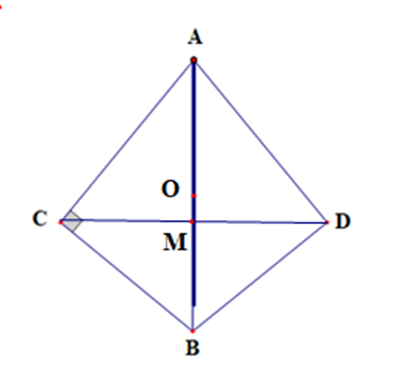
Cho tam giác ABC và ABD vuông có chung cạnh huyền AB ( C, D cùng
Cho tam giác ABC và ABD vuông có chung cạnh huyền AB ( C, D cùng thuộc 1 nua mp có bờ là AB).
a) Chứng minh A, B , C, D cùng thuộc 1 đường tròn và gọi đường tròn đó có tâm O
b) Chứng minh CD < AB.
c) Giả sử 2 đoạn thẳng CD cắt AB tại M. Chứng minh OM = \(\frac{{MA + MB}}{2}\).