Cho tam giác ABC, trọng tâm G. Vẽ đường thẳng d đi qua G cắt các đoạn thẳng AB, AC. Goi A', B', C' thứ tự là hình chiếu của A, B, C trên d. Tìm liên hệ giữa các độ dài AA', BB', CC'.

Trả lời

Lời giải

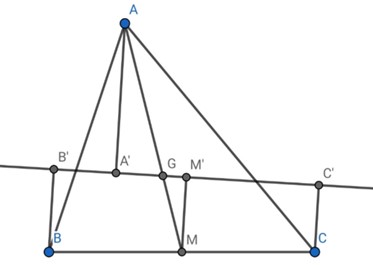
Gọi M là trung điểm của BC

M' là hình chiếu của M lên d

Þ MM' // BB' // CC'

Þ MM' là đường trung bình của hình thang vuông BB'C'C

\[ \Rightarrow MM' = \frac{1}{2}\left( {BB' + CC'} \right)\]

Xét ∆AA'G và ∆MM'G có:

\(\widehat {A'} = \widehat {M'} = 90^\circ \)

\[\widehat {A'AG} = \widehat {MM'G}\] (so le trong)

Do đó ∆AA'G ᔕ ∆MM'G (g.g)

\( \Rightarrow \frac{{AA'}}{{MM'}} = \frac{{AG}}{{GM}}\)

Áp dụng tính chất của trọng tâm, ta có:

\(\frac{{AG}}{{AM}} = \frac{2}{3} \Rightarrow \frac{{AG}}{{GM}} = 2\)

Do đó: \(\frac{{AA'}}{{MM'}} = 2\)

\( \Rightarrow AA' = 2MM' = 2 \cdot \frac{1}{2}\left( {BB' + CC'} \right) = BB' + CC'\)

Vậy AA' = BB' + CC'.