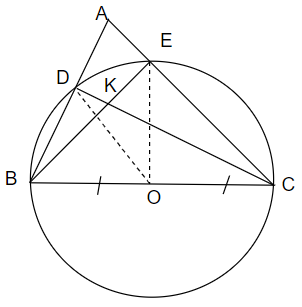
Cho tam giác ABC nhọn, vẽ đường tròn \(\left( {O;\frac{1}{2}BC} \right)\) cắt các cạnh AB, AC theo thứ tự tại D và E.

a) Chứng minh rằng: CD vuông góc với AB, BE vuông góc với AC.

b) Gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc với BC.

Lời giải

a) Tam giác BCD nội tiếp trong đường tròn (O) có BC là đường kính nên vuông tại D.

Suy ra: CD ⊥ AB.

Tam giác BCE nội tiếp trong đường tròn (O) có BC là đường kính nên vuông tại E.

Suy ra: BE ⊥ AC.

b) Xét ∆ABC có K là giao điểm của hai đường cao CD và BE nên K là trực tâm của tam giác ABC.