Cho tam giác ABC nhọn, đường cao AH. Gọi M, N lần lượt là hình chiếu

Đề bài. Cho tam giác ABC nhọn, đường cao AH. Gọi M, N lần lượt là hình chiếu cùa H lên AB và AC.

a) Chứng minh: AM.AB = AN.AC.

b) Chứng minh: $\frac{S_{AMN}}{S_{ACB}}={\sin }^{2}B.{\sin }^{2}C$

Trả lời

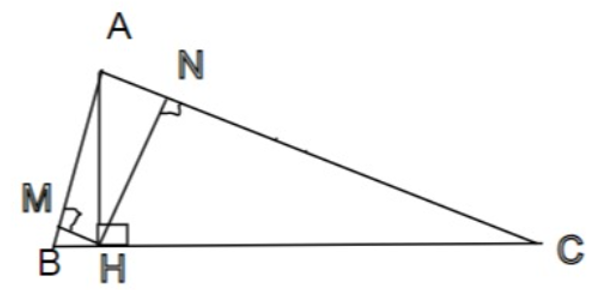a) Có : AH là đường cao của tam giác ABC ⇒ $\widehat{AHB}={90}^{\circ }$

Tam giác AHB vuông tại H có AM là đường cao

⇒ AM.AB = AH²

Tam giac AHC vuông tai H có AN là đường cao

⇒ AN.AC = AH²

Nên AM.AB =AN.AC

b) Tam giác AHB vuông tại H nên $\sin B=\frac{AH}{AB}$

Tam giác AHC vuông tại H ⇒ $\sin C=\frac{AH}{AC}$

Áp dụng công thức tính diện tích theo định lý sin, ta có:

Lại có: $S_{ABC}=\frac{1}{2}.AB.AC.\sin A$

$S_{AMN}=\frac{1}{2}.AM.AN.\sin A$

Suy ra: $\frac{S_{AMN}}{S_{ABC}}=\frac{\frac{1}{2}.AM.AN.\sin A}{\frac{1}{2}.AB.AC.\sin A}=\frac{AM.AN}{AB.AC}=\frac{A{H}^2.A{H}^2}{A{B}^2.A{C}^2}={\left(\frac{AH}{AB}\right)}^2.{\left(\frac{AH}{AC}\right)}^2={\sin }^{2}B.{\sin }^{2}C$