Cho tam giác ABC nhọn có góc A = 70^0 và điểm D thuộc cạnh BC. Gọi E là điểm đối xứng với D qua AB. Gọi F là điểm đối xứng với D qua AC. Đường thẳng EF cách AB, AC theo thứ tự tại M, N. a) T

Trả lời

Lời giải

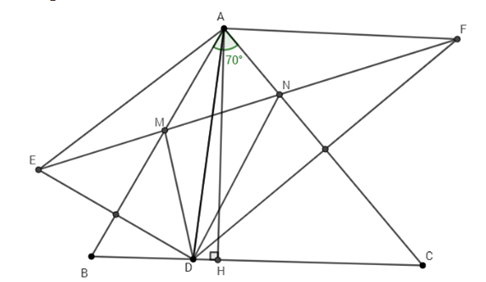
a) Vì E đối xứng D qua AB nên AB là trung trực của DE

Suy ra AE = AD

Do đó tam giác AED cân tại A

Mà AB là đường trung trực

Suy ra AB là phân giác của \(\widehat {DA{\rm{E}}}\)

Do đó \(\widehat {DAB} = \widehat {BA{\rm{E}}} = \frac{1}{2}\widehat {DA{\rm{E}}}\)

Vì F đối xứng D qua AC nên AC là trung trực của DF

Suy ra AF = AD

Do đó tam giác AFD cân tại A

Mà AC là đường trung trực

Suy ra AC là phân giác của \(\widehat {DAF}\)

Do đó \(\widehat {DAC} = \widehat {CAF} = \frac{1}{2}\widehat {DAF}\)

Ta có \(\widehat {F{\rm{AE}}} = \widehat {F{\rm{AD}}} + \widehat {DAE} = 2\widehat {CA{\rm{D}}} + 2\widehat {BAD} = 2\widehat {BAC} = 2.70^\circ = 140^\circ \)

Ta có AF = AE (= AD)

Suy ra tam giác AFE cân tại A, do đó \[\widehat {{\rm{AFE}}} = \widehat {{\rm{AEF}}}\]

Xét tam giác AEF có

\[\widehat {{\rm{AFE}}} + \widehat {{\rm{AEF}}} + \widehat {F{\rm{AE}}} = 180^\circ \] (tổng ba góc trong một tam giác)

Mà \[\widehat {{\rm{AFE}}} = \widehat {{\rm{AEF}}},\widehat {FA{\rm{E}}} = 140^\circ \] (chứng minh trên)

Suy ra \[\widehat {{\rm{AFE}}} = \widehat {{\rm{AEF}}} = \frac{{180^\circ - 140^\circ }}{2} = 20^\circ \]

b) Xét DAME và DAMD có

AM là cạnh chung;

\(\widehat {E{\rm{A}}M} = \widehat {DAM}\)(chứng minh trên);

AD = AE (chứng minh trên)

Do đó DAME = DAMD (c.g.c)

Suy ra \(\widehat {{\rm{AE}}M} = \widehat {ADM}\) (hai góc tương ứng)

Xét DANF và DAND có

AN là cạnh chung;

\(\widehat {{\rm{FAN}}} = \widehat {DAN}\)(chứng minh trên);

AD = AF (chứng minh trên)

Do đó DANF = DAND (c.g.c)

Suy ra \(\widehat {{\rm{AFN}}} = \widehat {ADN}\) (hai góc tương ứng)

Mà \(\widehat {{\rm{AE}}M} = \widehat {ADM}\), \[\widehat {{\rm{AFE}}} = \widehat {{\rm{AEF}}}\]

Suy ra \(\widehat {{\rm{ADM}}} = \widehat {ADN}\)

Do đó DA là tia phân giác của góc MDN.

c) Gọi giao điểm của DE và AB là P, giao điểm của DF và AC là Q

Khi đó P là trung điểm của DE, Q là trung điểm của DF

Xét tam giác DFE có P, Q lần lượt là trung điểm của DE, DF

Suy ra PQ là đường trung bình

Do đó PQ // FE và \(PQ = \frac{1}{2}F{\rm{E}}\)

Vì M thuộc trung trực của DE nên MD = ME

Vì N thuộc trung trực của DF nên ND = NF

Chu vì tam giác DMN là

DM + DN + MN = ME + NF + MN = FE

Để chu vi tam giác DMN nhỏ nhất

⇔ FE nhỏ nhất

⇔ PQ nhỏ nhất (vì \(PQ = \frac{1}{2}F{\rm{E}}\))

⇔ PQ // BC và \(PQ = \frac{1}{2}BC\)

⇔ PQ là đường trung bình của tam giác ABC

⇔ D là trung điểm của BC

Vậy D là trung điểm của BC thì chu vi tam giác DMN nhỏ nhất.