Cho tam giác ABC nhọn. Chứng minh rằng BC^2 = AB^2 + AC^2 – 2AB.AC.cosA
Đề bài: Cho tam giác ABC nhọn. Chứng minh rằng BC2 = AB2 + AC2 – 2AB.AC.cosA.
Hướng dẫn giải:
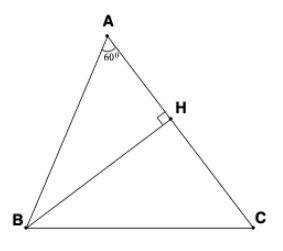
Kẻ đường cao BH
Xét tam giác ABH vuông ở H có AH = AB.cosA
Theo định lí Pytago ta có
AB2 = AH2 + BH2
Xét tam giác ACH vuông ở H có AC2 = AH2 + CH2 (định lí Pytago)
Ta có AB2 + AC2 – 2AB.AC.cosA
= AB2 + AC2 – 2AC.AH
= AH2 + BH2 + AC2 – 2AC.AH
= BH2 + (AC – AH)2
= BH2 + HC2
= BC2
Vậy BC2 = AB2 + AC2 – 2AB.AC.cosA.