Cho tam giác ABC nhọn (AB < AC), đường cao AH. Gọi M, N lần lượt là hình chiếu của H trên AB, AC. Tính AH, MH biết AM = 8 cm; BM = 2 cm.
27
22/05/2024
Cho tam giác ABC nhọn (AB < AC), đường cao AH. Gọi M, N lần lượt là hình chiếu của H trên AB, AC. Tính AH, MH biết AM = 8 cm; BM = 2 cm.
Trả lời
Lời giải
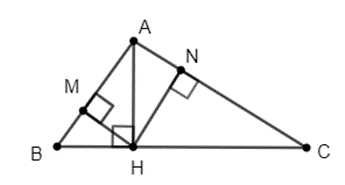
Xét ∆AHB vuông tại H có đường cao MH nên ta có: MH2 = MB.MA.
Do đó \(MH = \sqrt {8\,.\,2} = \sqrt {16} = 4\) (cm).
Áp dụng định lý Py−ta−go vào ∆AMH vuông tại M, ta có:
\(AH = \sqrt {A{M^2} + \;M{H^2}} = \sqrt {{8^2} + {4^2}} = 4\sqrt 5 \) (cm).
Vậy \(AH = 4\sqrt 5 \) cm; MH = 4 cm.

