Cho tam giác ABC nhọn AB < AC. Các đường cao BE, CF cắt nhau tại H

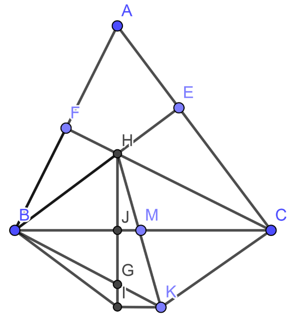
Đề bài. Cho tam giác ABC nhọn AB < AC. Các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC. Kẻ Bx, Cy lần lượt vuông góc với AB, AC chúng cắt nhau tại K.

1. Chứng minh tứ giác BHCK là hình bình hành và H, M, K thẳng hàng

2. Gọi I là điểm đối xứng với H qua BC. Chứng minh tứ giác BIKC là hình thang cân

3. Gọi G là giao điểm của BK và HI, tam giác ABC phải có thêm điều kiện gì để tứ giác GHCK là hình thang cân.

Trả lời

1) Ta có: BH vuông góc với AC

CK vuông góc với AC

⇒ BH // CK

Chứng minh tương tự ta có: CH // BK

Xét tứ giác BHCK có: BH // CK; CH//BK

⇒ Tứ giác BHCK là hình bình hành

Có M là trung điểm của BC⇒ M là trung điểm của HK

⇒ M, H, K thẳng hàng

2. Gọi HI cắt BC tại J

Xét tam giác HIK có: J là trung điểm của HI; M là trung điểm của HK

⇒ JM là đường trung bình trong tam giác HIK

⇒ IK // MJ hay IK // BC

Xét tam giác BHJ và tam giác BIJ có;

HJ = JI

$\widehat{BJH}=\widehat{BJI}={90}^{\circ }$

BJ chung

⇒ ∆BHJ = ∆BIJ (c.g.c)

⇒ $\widehat{HBJ}=\widehat{IBJ}$

Mà $\widehat{HBJ}=\widehat{BCK}$(do BH//CK)

Xét tứ giác BIKC có: KI // BC

$\widehat{IBC}=\widehat{KCB}$

⇒Tứ giác BIKC là hình thang cân

3. Xét tứ giác GHCK có: GK//HC (do BK // HC)

⇒ Tứ giác GHCK là hình thang

Để GHCK là hình thang cân ⇒ $\widehat{GHC}=\widehat{KCH}$(1)

mà $\widehat{GHC}+\widehat{HCB}={90}^{\circ }$

$\widehat{KCH}+\widehat{HCA}={90}^{\circ }$

⇒ (1) $\widehat{HCB}=\widehat{HCA}$CH là phân giác của góc $\widehat{ACB}$

Xét tam giác ABC có : CH là phân giác của góc $\widehat{ACB}$

CH là đường cao trong tam giác ABC

⇒ Tam giác ABC cân tại C

Vậy tứ giác GHCK là hình thang cân

⇒ Tam giác ABC cân tại C