Cho tam giác ABC, I là giao điểm của 3 đường phân giác, đường thẳng vuông góc với CI tại I cắt AC và BC tại M và N.

a) Chứng minh AM.BI = AI.IM.

b) Chứng minh BN.AI = BI.NI.

c) Chứng minh \(\frac{{AM}}{{BN}} = {\left( {\frac{{AI}}{{BI}}} \right)^2}\).

Lời giải

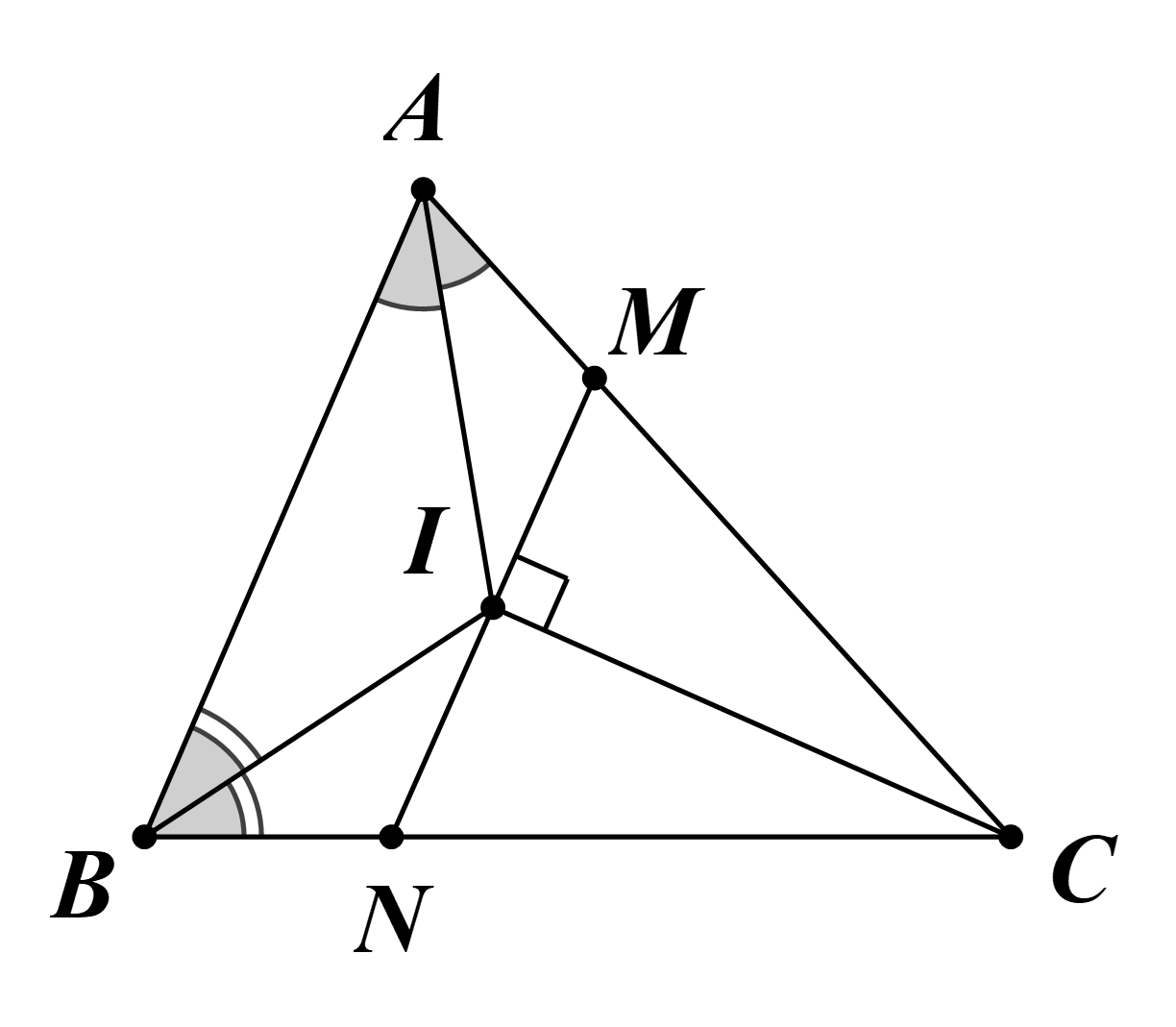
a) Vì AI, BI, CI là ba đường phân giác của tam giác ABC nên ta có:

 \(\widehat {AIB} = 180^\circ - \widehat {IAB} - \widehat {IBA} = 180^\circ - \frac{1}{2}\widehat {BAC} - \frac{1}{2}\widehat {ABC}\)

\[ = 180^\circ - \frac{1}{2}\left( {\widehat {BAC} + \widehat {ABC}} \right) = 180^\circ - \frac{1}{2}\left( {180^\circ - \widehat {ACB}} \right)\]

\[ = 180^\circ - \frac{1}{2}\left( {180^\circ - 2\widehat {ACI}} \right) = 90^\circ + \widehat {ACI}\].

Lại có \(\widehat {AMI} = \widehat {MIC} + \widehat {ACI} = 90^\circ + \widehat {ACI}\) (tính chất góc ngoài của tam giác).

Suy ra \(\widehat {AIB} = \widehat {AMI}\).

Xét ∆AIM và ∆ABI, có:

\(\widehat {AIB} = \widehat {AMI}\) (chứng minh trên);

\(\widehat {BAI} = \widehat {IAM}\) (do AI là tia phân giác của \(\widehat {BAC}\)).

Do đó (g.g).

Suy ra \(\frac{{AM}}{{AI}} = \frac{{IM}}{{BI}}\).

Vậy AM.BI = AI.IM (điều phải chứng minh).

b) Chứng minh tương tự câu a, ta có (g.g).

Suy ra \(\frac{{BN}}{{BI}} = \frac{{IN}}{{AI}}\).

Vậy BN.AI = BI.NI (điều phải chứng minh).

c) Ta có (chứng minh trên).

Suy ra \(\frac{{AI}}{{AB}} = \frac{{AM}}{{AI}}\).

⇔ AI² = AB.AM    (1)

Lại có (chứng minh trên).

Suy ra \(\frac{{BI}}{{AB}} = \frac{{BN}}{{BI}}\).

⇔ BI² = AB.BN    (2)

Từ (1), (2), suy ra \(\frac{{A{I^2}}}{{B{I^2}}} = \frac{{AB.AM}}{{AB.BN}}\).

\( \Leftrightarrow \frac{{AM}}{{BN}} = {\left( {\frac{{AI}}{{BI}}} \right)^2}\).

Vậy ta có điều phải chứng minh.