Lời giải
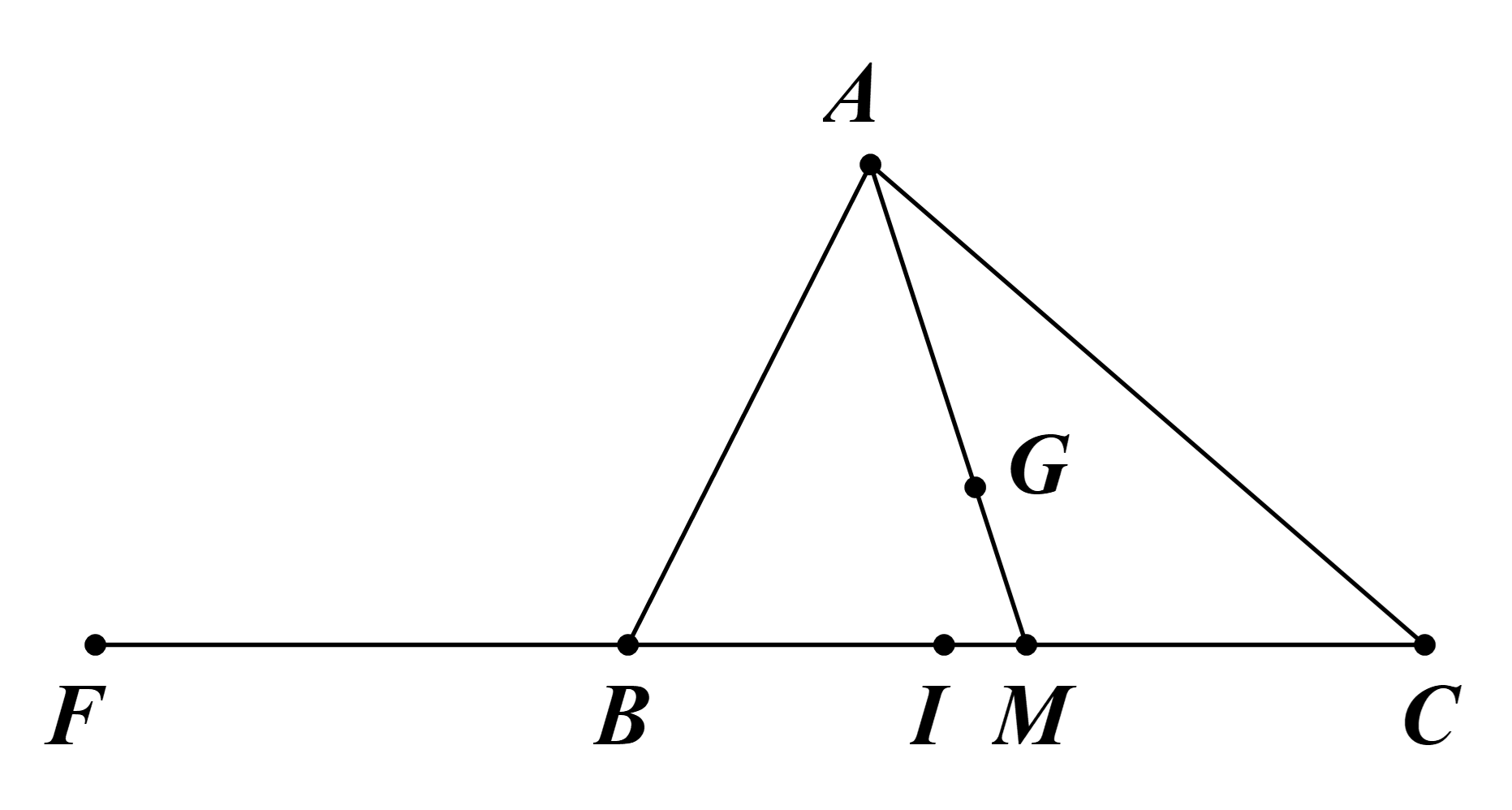
a) Ta có 2CI = 3BI
\( \Rightarrow 2\overrightarrow {CI} + 3\overrightarrow {BI} = \vec 0\)
\( \Leftrightarrow 2\left( {\overrightarrow {CA} + \overrightarrow {AI} } \right) + 3\left( {\overrightarrow {BA} + \overrightarrow {AI} } \right) = \vec 0\)
\( \Leftrightarrow 5\overrightarrow {AI} = 3\overrightarrow {AB} + 2\overrightarrow {AC} \) (1)
\( \Leftrightarrow \overrightarrow {AI} = \frac{3}{5}\overrightarrow {AB} + \frac{2}{5}\overrightarrow {AC} \).
Ta có 5FB = 2FC
\( \Rightarrow 5\overrightarrow {BF} - 2\overrightarrow {CF} = \vec 0\)
\( \Leftrightarrow 5\left( {\overrightarrow {BA} + \overrightarrow {AF} } \right) - 2\left( {\overrightarrow {CA} + \overrightarrow {AF} } \right) = \vec 0\)
\( \Leftrightarrow 3\overrightarrow {AF} = 5\overrightarrow {AB} - 2\overrightarrow {AC} \) (2)
\( \Leftrightarrow \overrightarrow {AF} = \frac{5}{3}\overrightarrow {AB} - \frac{2}{3}\overrightarrow {AC} \).
Vậy \(\overrightarrow {AI} = \frac{3}{5}\overrightarrow {AB} + \frac{2}{5}\overrightarrow {AC} \) và \(\overrightarrow {AF} = \frac{5}{3}\overrightarrow {AB} - \frac{2}{3}\overrightarrow {AC} \).
b) Gọi M là trung điểm của BC.
Suy ra \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} = 2.\frac{3}{2}.\overrightarrow {AG} = 3\overrightarrow {AG} \) (do G là trọng tâm của tam giác ABC nên \(AG = \frac{2}{3}AM\)).
Lấy (1) + (2) vế theo vế, ta được \(5\overrightarrow {AI} + 3\overrightarrow {AF} = 8\overrightarrow {AB} \).
\( \Leftrightarrow \overrightarrow {AB} = \frac{5}{8}\overrightarrow {AI} + \frac{3}{8}\overrightarrow {AF} \).
Từ (1), ta suy ra \[25\overrightarrow {AI} = 15\overrightarrow {AB} + 10\overrightarrow {AC} \] (3)
Từ (2), ta suy ra \(9\overrightarrow {AF} = 15\overrightarrow {AB} - 6\overrightarrow {AC} \) (4)
Lấy (3) – (4) vế theo vế, ta được \[16\overrightarrow {AC} = 25\overrightarrow {AI} - 9\overrightarrow {AF} \].
\( \Leftrightarrow \overrightarrow {AC} = \frac{{25}}{{16}}\overrightarrow {AI} - \frac{9}{{16}}\overrightarrow {AF} \).
Gọi M là trung điểm của BC.
Suy ra \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} = 2.\frac{3}{2}.\overrightarrow {AG} = 3\overrightarrow {AG} \) (do G là trọng tâm của tam giác ABC nên \(AG = \frac{2}{3}AM\)).
Do đó \(3\overrightarrow {AG} = \left( {\frac{5}{8}\overrightarrow {AI} + \frac{3}{8}\overrightarrow {AF} } \right) + \left( {\frac{{25}}{{16}}\overrightarrow {AI} - \frac{9}{{16}}\overrightarrow {AF} } \right) = \frac{{35}}{{16}}\overrightarrow {AI} - \frac{3}{{16}}\overrightarrow {AF} \).
Vậy \(\overrightarrow {AG} = \frac{{35}}{{48}}\overrightarrow {AI} - \frac{1}{{16}}\overrightarrow {AF} \).

