Cho tam giác ABC. Gọi O là một điểm thuộc miền trong tam giác. Gọi M, N, P, Q lần lượt là trung điểm của OB, OC, AC, AB.

a) Chứng minh rằng MNPQ là hình bình hành.

b) Xác định vị trí O để MNPQ là hình chữ nhật.

Lời giải

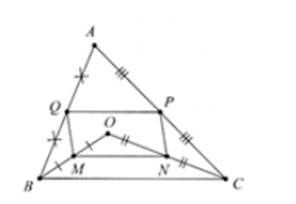
a) Xét tam giác ABO có Q là trung điểm của AB, M là trung điểm của OB

Suy ra QM là đường trung bình

Suy ra QM // AO, \({\rm{QM = }}\frac{1}{2}{\rm{AO}}\)                               (1)

Xét tam giác ACO có P là trung điểm của AC, N là trung điểm của OC

Suy ra PN là đường trung bình

Suy ra PN // AO, \({\rm{PN = }}\frac{1}{2}{\rm{AO}}\)                               (2)

Từ (1) và (2) suy ra QM // PN, QM = PN

Do đó MNPQ là hình bình hành

Vậy MNPQ là hình bình hành

b) Xét tam giác ABC có P là trung điểm của AC, Q là trung điểm của AB

Suy ra PQ là đường trung bình

Suy ra PQ // BC

Để hình bình hành MNPQ là hình chữ nhật

⇔ QM ⊥ QP

⇔ QM ⊥ BC (vì QP // BC)

⇔ AO ⊥ BC (vì QM // AO)

⇔ O thuộc đường thẳng qua A và vuông góc BC

Vậy O thuộc đường thẳng qua A và vuông góc BC thì MNPQ là hình chữ nhật.