Cho tam giác ABC. Gọi H là trực tam của tam giác. Chứng minh rằng

Câu 18: Cho tam giác ABC. Gọi H là trực tam của tam giác. Chứng minh rằng:

AH² + BC² = BH² + AC²

Trả lời

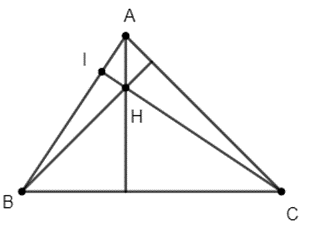
Gọi I là giao điểm của CH và AB.

Áp dụng định lý Py-ta-go cho các tam giác vuông ∆AHI, ∆BHI, ∆ACI, ∆BCI ta có:

AH² = AI² + HI² ⇒ AH² – AI² = HI²

BH² = IH² + BI² ⇒ BH² – BI² = IH²

AC² = AI² + IC² ⇒ AC² – AI² = IC²

BC² = BI² + IC² ⇒ BC² – BI² = IC² 

Suy ra:

AH² – AI² = BH² – BI² (1)

AC² – AI² = BC² – BI² (2)

Trừ (2) cho (1) ta được:

AC² – AH² = BC² – BH²

⇒ AH² + BC² = BH² + AC² (đpcm)