Câu 44: Cho tam giác ABC điểm M nằm trong tam giác. Gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB. Gọi A’, B’, C’ thứ tự là điểm đối xứng của M qua D, E, F
a) Chứng minh tứ giác AB’A’B là hình bình hành.
b) Gọi O là giao điểm của AA’ và BB’, chứng minh C và C’ đối xứng nhau qua điểm O.
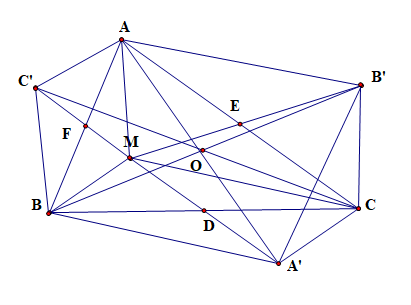
a) Xét tứ giác AB’CM có
AC cắt MB' tại trung điểm E của mỗi đường và AC, MB’ là hai đường chéo
Suy ra AB'CM là hình bình hành
Do đó AB' // MC, AB' = MC
Xét tứ giác BMCA’ có
BC cắt MA' tại trung điểm D của mỗi đường và BC, MA’ là hai đường chéo
Suy ra BMCA' là hình bình hành
Do đó MC // A'B, MC = A'B.
Ta có AB' // MC, MC // A'B (chứng minh trên), suy ra AB’ // A’B.
Ta có MC = A'B, AB' = MC (chứng minh trên), suy ra AB’ = A’B.
Xét tứ giác AB’A’B có AB’ // A’B và AB’ = A’B
Suy ra tứ giác AB'A'B là hình bình hành.
b) Xét hình bình hành AB'A'B có AA’ và BB’ cắt nhau tại O
Suy ra O là trung điểm của AA’.
Chứng minh tương tự câu a ta có: AC’ = A’C (= BM) và AC’ // A’C (// BM)
Suy ra AC’A’C là hình bình hành.
Mà O là trung điểm của AA’
Suy ra O là trung điểm của CC’.
Hay C và C’ đối xứng nhau qua điểm O
Vậy C và C’ đối xứng nhau qua điểm O.