Lời giải

Đáp án đúng là A

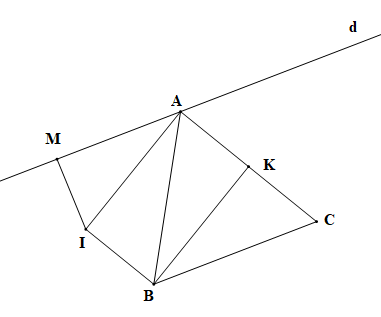
Gọi K là trung điểm của AC

Vì tam giác ABC đều nên BK là tia phân giác của góc ABC, \(\widehat {ABC} = 60^\circ \)

Suy ra \(\widehat {ABK} = 30^\circ \)

Xét tam giác ABC đều cạnh 2a có K là trung điểm của AC

Nên BK là đường cao, AB = 2a, AK = a

Suy ra tam giác ABK vuông tại K

Do đó AB² = BK² + AK²

Hay (2a)² = BK² + a²

Suy ra BK = a\(\sqrt 3 \)

Xét điểm I sao cho \(\overrightarrow {IA} + 2\overrightarrow {IB} - \overrightarrow {IC} = \overrightarrow 0 \)

\( \Leftrightarrow \overrightarrow {IA} + 2(\overrightarrow {IA} + \overrightarrow {AB} ) - (\overrightarrow {IA} + \overrightarrow {AC} ) = \overrightarrow 0 \)

\( \Leftrightarrow \overrightarrow {IA} + 2\overrightarrow {IA} + 2\overrightarrow {AB} - \overrightarrow {IA} - \overrightarrow {AC} = \overrightarrow 0 \)

\( \Leftrightarrow 2\overrightarrow {IA} + 2\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow 0 \)

\( \Leftrightarrow 2\overrightarrow {IA} + \overrightarrow {AB} + \overrightarrow {CB} = \overrightarrow 0 \)

\( \Leftrightarrow \overrightarrow {IA} = \frac{{\overrightarrow {BA} + \overrightarrow {BC} }}{2}\)

\( \Leftrightarrow \overrightarrow {IA} = \overrightarrow {BK} \)

Suy ra I là đỉnh thứ 4 của hình bình hành AIBK

Do đó AI // BK, AI = BK

Suy ra \(\widehat {IAB} = \widehat {ABK}\) (hai góc so le trong)

Mà \(\widehat {ABK} = 30^\circ \) nên \(\widehat {IAB} = 30^\circ \)

Ta có: \(\left| {\overrightarrow {MA} + 2\overrightarrow {MB} - \overrightarrow {MC} } \right|\) = \(\left| {(\overrightarrow {MI} + \overrightarrow {IA} ) + 2(\overrightarrow {MI} + \overrightarrow {IB} ) - (\overrightarrow {MI} + \overrightarrow {IC} )} \right|\)

= \(\left| {2\overrightarrow {MI} + (\overrightarrow {IA} + 2\overrightarrow {IB} - \overrightarrow {IC} )} \right|\) = \(\left| {2\overrightarrow {MI} } \right|\) = 2MI

Vì M ∈ d nên \(\left| {\overrightarrow {MA} + 2\overrightarrow {MB} - \overrightarrow {MC} } \right|\) đạt giá trị nhỏ nhất khi MI ⊥ d

Khi đó \(\widehat {MAI} = \widehat {MAB} - \widehat {IAB} = 60^\circ - 30^\circ = 30^\circ \)

Xét tam giác AMI vuông tại M có

IM = IA. sin\(\widehat {MAI}\)= BK. sin 30° = \(\frac{{BK}}{2}\)= \(\frac{{a\sqrt 3 }}{2}\)

Suy ra \(\left| {\overrightarrow {MA} + 2\overrightarrow {MB} - \overrightarrow {MC} } \right|\) = 2IM = \(a\sqrt 3 \)

Vậy ta chọn đáp án A.