Cho tam giác ABC có góc B = góc C. Tia phân giác của góc A cắt BC tại D
Cho tam giác ABC có \(\widehat B = \widehat C\) . Tia phân giác của góc A cắt BC tại D. Chứng minh rằng:
a) Tam giác ADB bằng tam giác ADC
b) AB = AC.
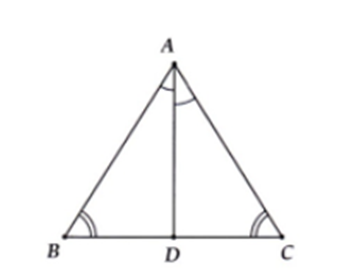
a) Xét tam giác ABC có \(\widehat B = \widehat C\)
Suy ra tam giác ABC cân tại A
Do đó AB = AC
Vì AD là tia phân giác của góc BAC
Nên \(\widehat {BA{\rm{D}}} = \widehat {CA{\rm{D}}}\)
Xét ΔADC và ΔADB có:
\(\widehat {BA{\rm{D}}} = \widehat {CA{\rm{D}}}\) (chứng minh trên)
AB = AC (chứng minh trên)
\(\widehat B = \widehat C\) (giả thiết)
Suy ra ΔADC = ΔADB (g.c.g)
Vậy ΔADC = ΔADB
b) Theo chứng minh câu a ta có AB = AC.