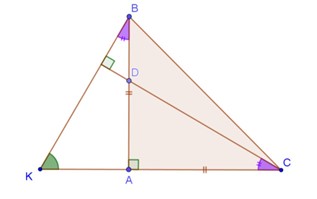
Cho tam giác ABC có góc A = 90^0, AB = AC, điểm D thuộc cạnh AB. Đường thẳng qua B và vuông góc với CD cắt đường thẳng CA ở K. Chứng minh rằng AK = AD

Trả lời

Lời giải

Xét ∆AKB vuông tại A và ∆ADC vuông tại A, ta có:

AB = AC (gt)

\(\widehat {ABK} = \widehat {ACD}\) (cùng phụ với \(\widehat K\))

Þ ∆AKB = ∆ADC (cạnh góc vuông - góc nhọn).

Þ AK = AD (hai cạnh tương ứng).