Lời giải
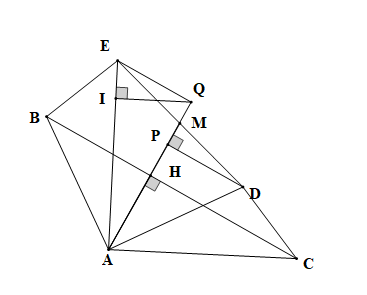
a) Ta có \(\widehat {BAE} + \widehat {EAD} = \widehat {BAD} = 90^\circ \)
\(\widehat {CA{\rm{D}}} + \widehat {EAD} = \widehat {CAE} = 90^\circ \)
Suy ra \(\widehat {BA{\rm{E}}} = \widehat {CAD}\)
Xét tam giác ABE và tam giác ADC có
AB = AD (giả thiết)
\(\widehat {BA{\rm{E}}} = \widehat {CAD}\)(chứng minh trên)
AC = AE (giả thiết)
Suy ra △ ABE = △ ADC (c.g.c)
Do đó \(\widehat {BEA} = \widehat {ACD}\)
Vì tam giác AEC vuông cân tại A
Nên \(\widehat {CEA} = \widehat {ACE} = \frac{{90^\circ }}{2} = 45^\circ \)
Mà \(\widehat {BEA} = \widehat {ACD}\)
Suy ra \(\widehat {BEA} = \widehat {AEC} = 45^\circ \)
Suy ra \(\widehat {BEA} + \widehat {AEC} = \widehat {BEC} = 45^\circ + 45^\circ = 90^\circ \)
Hay BE ⊥ DC
b) Ta có \(\widehat {BAH} + \widehat {HAD} = \widehat {BAD} = 90^\circ \)
Vì tam giác ABH vuông tại H nên \(\widehat {BAH} + \widehat {HBA} = 90^\circ \) (trong tam giác vuông tổng hai góc nhọn bằng 90°)
Suy ra \(\widehat {DAH} = \widehat {HBA}\)
Vì tam giác ADP vuông tại H nên \(\widehat {PA{\rm{D}}} + \widehat {P{\rm{D}}A} = 90^\circ \) (trong tam giác vuông tổng hai góc nhọn bằng 90°)
Suy ra \(\widehat {BAH} = \widehat {P{\rm{D}}A}\)
Xét tam giác ABH và tam giác DAP có
\(\widehat {DAH} = \widehat {HBA}\) (chứng minh trên)
AB = AD (giả thiết)
\(\widehat {BAH} = \widehat {P{\rm{D}}A}\)(chứng minh trên)
Suy ra △ ABH = △ DAP (g.c.g)
Do đó AH = DP (hai góc tương ứng)
Vậy AH = DP.
c) Ta có \(\widehat {EAQ} + \widehat {CAQ} = \widehat {EAC} = 90^\circ \)
Vì tam giác AEQ vuông tại Q nên \(\widehat {QAE} + \widehat {QEA} = 90^\circ \) (trong tam giác vuông tổng hai góc nhọn bằng 90°)
Suy ra \(\widehat {CAQ} = \widehat {QEA}\)
Xét tam giác AEQ và tam giác CAH có
\(\widehat {AQE} = \widehat {CHA}\left( { = 90^\circ } \right)\)
AE = AC (giả thiết)
\(\widehat {CAQ} = \widehat {QEA}\) (chứng minh trên)
Suy ra △ AEQ = △ CAH (cạnh huyển – góc nhọn)
Do đó AH = EQ (hai góc tương ứng)
Mà AH = DP (chứng minh câu b)
Suy ra EQ = DP
Ta có EQ ⊥ AM, DP ⊥ AM
Suy ra EQ // PD
Xét tứ giác EQDP có EQ // PD, EQ = DP
Suy ra EQDP là hình bình hành
Mà DE cắt PQ ở M
Suy ra M là trung điểm của DE
Vậy M là trung điểm của DE.
d) Vì tam giác AQE vuông ở Q nên AE2 = EQ2 + AQ2
Hay AE2 = 32 + 42 = 9 + 16 = 25
Suy ra AE = 5
Xét tam giác AEQ vuông tại Q có QI ⊥ AE
Suy ra EQ2 = EI . EA (hệ thức lượng trong tam giác vuông)
Hay 32 = EI . 5
Suy ra EI = 1,8
Ta có AI = AE – EI = 5 – 1,8 = 3,2
Vậy EI = 1,8 cm và AI = 3,2 cm.

