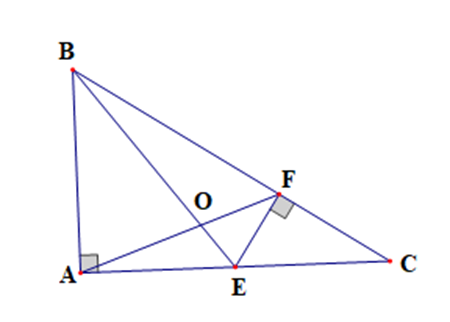
a) Xét tam giác CEF vuông ở F có \(\cos C = \frac{{CF}}{{CE}}\)

Xét tam giác CEF và tam giác CBA có

\(\widehat C\) là góc chung;

\(\widehat {BAC} = \widehat {{\rm{EF}}C} = 90^\circ \)

Suy ra  (g.g)

Do đó \(\frac{{CF}}{{CE}} = \frac{{CA}}{{CB}}\)

Xét tam giác AFC và tam giác BEC có

\(\widehat C\) là góc chung;

\(\frac{{CF}}{{CE}} = \frac{{CA}}{{CB}}\) (chứng minh trên)

Suy ra  (g.g)

Do đó \(\frac{{CF}}{{CE}} = \frac{{FA}}{{BE}}\)

Mà cosC = \(\frac{{CF}}{{CE}}\)

Suy ra AF = BE . cosC.

b) Vì tam giác ABC vuông tại A

Suy ra AB = BC . sinC = 10 . 0,6 = 6.

Xét tam giác ABC vuông tại A, theo định lí Pytago có

BC² = AB² + AC²

Suy ra \(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\)

Mà E là trung điểm AC nên AE = EC = 4

Vì tam giác FEC vuông tại F

Suy ra FE = EC . sinC = 4 . 0,6 = 2,4

Xét tam giác FEC vuông tại F, theo định lí Pytago có

EC² = FE² + FC²

Suy ra \(FC = \sqrt {E{C^2} - F{{\rm{E}}^2}} = \sqrt {{4^2} - 2,{4^2}} = 3,2\)

Khi đó BF = BC – FC = 10 – 3,2 = 6,8

Ta có S_ABFE = S_ABE + S_BFE

\( = \frac{1}{2}AB.AE + \frac{1}{2}BF.FE\)

\( = \frac{1}{2}.6.4 + \frac{1}{2}.6,8.2,4 = 20,16\left( {c{m^2}} \right)\)

c) Ta có \(\frac{{CF}}{{CE}} = \frac{{FA}}{{BE}} = \frac{{3,2}}{4}\)

Suy ra AF = 0,8BE

Vì tam giác ABE vuông tại A nên

BE² = AB² + AE²

Hay BE² = 6² + 4²

suy ra \(BE = \sqrt {52} \)

Ta có \[{S_{ABFE}} = \frac{1}{2}AF.BE.\sin \widehat {AOB}\]

\( \Leftrightarrow 20,16 = \frac{1}{2}.0,8.\sqrt {52} .\sqrt {52} .\sin \widehat {AOB}\)

\( \Leftrightarrow \sin \widehat {AOB} = \frac{{20,16}}{{20,8}} = \frac{{63}}{{65}}\) .