Cho tam giác ABC có góc A= 65 độ, góc B= 54 độ. Vẽ trực tâm H của tam giác ABC. Tính góc AHB.

Bài 4 trang 63 SBT Toán 7 Tập 2: Cho tam giác ABC có $\widehat{A}=65°,\widehat{B}=54°$. Vẽ trực tâm H của tam giác ABC. Tính góc AHB.

Trả lời

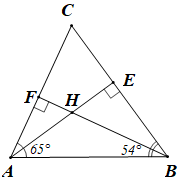
Trong tam giác vuông ABE ta có: $\widehat{E\text{A}B}+\widehat{EBA}=90°$ (trong một tam giác vuông, tổng hai góc nhọn bằng 90°).

Mà $\widehat{EBA}=54°$ nên $\widehat{EAB}=90°-\widehat{EBA}=90°-54°=36°$.

Trong tam giác vuông BAF ta có: $\widehat{\text{FA}B}+\widehat{FBA}=90°$ (trong một tam giác vuông, tổng hai góc nhọn bằng 90°).

Mà $\widehat{FAB}=65°$ nên $\widehat{FBA}=90°-\widehat{FAB}=90°-65°=25°$.

Trong $∆$AHB ta có: $\widehat{HAB}+\widehat{HBA}+\widehat{AHB}=180°$ (tổng ba góc trong một tam giác).

Suy ra $\widehat{AHB}=180°-\widehat{HAB}-\widehat{HBA}$$=180°-36°-25°=119°$.

Vậy $\widehat{AHB}=119°.$

Xem thêm lời giải sách bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 6: Tính chất ba đường trung trực của tam giác

Bài 7: Tính chất ba đường trung tuyến của tam giác

Bài 8: Tính chất ba đường cao của tam giác

Bài 9: Tính chất ba đường phân giác của tam giác

Bài tập cuối chương 8

Bài 1: Làm quen với yếu tố ngẫu