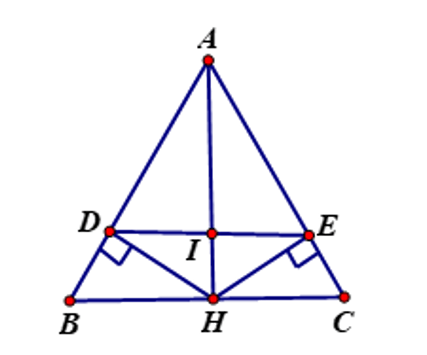
Cho tam giác ABC có AB = AC và tia phân giác góc A cắt BC ở H.

a) Chứng minh $\text{ΔABH = ΔACH}$

b) Chứng minh AH ⊥ BC

c) Vẽ $\text{HD }\perp \text{AB (D }\in \text{AB)}$ và $HE\perp AC(E\in AC)$. Chứng minh: DE // BC

a) Xét $\Delta ABH$ và $\Delta BCH$  có:

AH cạnh chung

$\widehat{BAH}=\widehat{CAH}$ (AH là tia phân giác của góc BAC)

AB = AC (gt)

Suy ra: $\text{ΔABH = ΔACH}\left(c–g–c\right)$

b) Ta có $\widehat{AHB}=\widehat{AHC}$ vì $\Delta ABH=\Delta ACH$)

Mà: $\widehat{AHB}+\widehat{AHC}={180}^0$ (kề bù)

Suy ra: $\widehat{AHB}=\widehat{AHC}={90}^0$ hay $AH\perp BC$ (1)

c) Gọi I là giao điểm của AH và DE

Xét hai tam giác vuông: $\Delta ADH$ và $\Delta AEH$ có:

AH cạnh chung

$\widehat{BAH}=\widehat{CAH}$ (AH là tia phân giác của góc BAC)

Suy ra: $\text{ΔADH = ΔAEH}$ (ch – gn)

Xét $\Delta ADI$ và $\Delta AẸI$ có:

AI: cạnh chung

$\widehat{BAH}=\widehat{CAH}$ (AH là tia phân giác của góc BAC)

$\text{AD = AE }\left(\text{ΔADH = ΔAEH}\right)$

Suy ra: $\Delta ADI=\Delta AEI$(c – g – c)

Suy ra $\widehat{\text{AID}}\text{ = }\widehat{\text{AIE}}$ (2 góc tương ứng)

Mà $\widehat{\text{AID}}\text{ = }\widehat{\text{AIE}}{\text{=180}}^0$ (kề bù)

Suy ra $\widehat{\text{AID}}\text{ = }\widehat{\text{AIE}}={90}^0$ hay $AH\perp DE$ (2)

Từ (1) và (2) suy ra DE // BC