Cho tam giác ABC có A’, B’, C’ lần lượt là trung điểm của các cạnh BC, CA, AB. Khẳng định nào sau đây là sai? A. vecto BC' = vecto C'A = vecto A'B'; B. vecto B'C' = vecto A'B = vecto CA';
30
14/05/2024
Cho tam giác ABC có A’, B’, C’ lần lượt là trung điểm của các cạnh BC, CA, AB. Khẳng định nào sau đây là sai?
A. \(\overrightarrow {BC'} = \overrightarrow {C'A} = \overrightarrow {A'B'} \);
B. \(\overrightarrow {B'C'} = \overrightarrow {A'B} = \overrightarrow {CA'} \);
C. \(\overrightarrow {C'A'} = \frac{1}{2}\overrightarrow {AC} \);
D. \(\overrightarrow {BA} + \overrightarrow {AB'} = \overrightarrow {AA'} \).
Trả lời
Lời giải
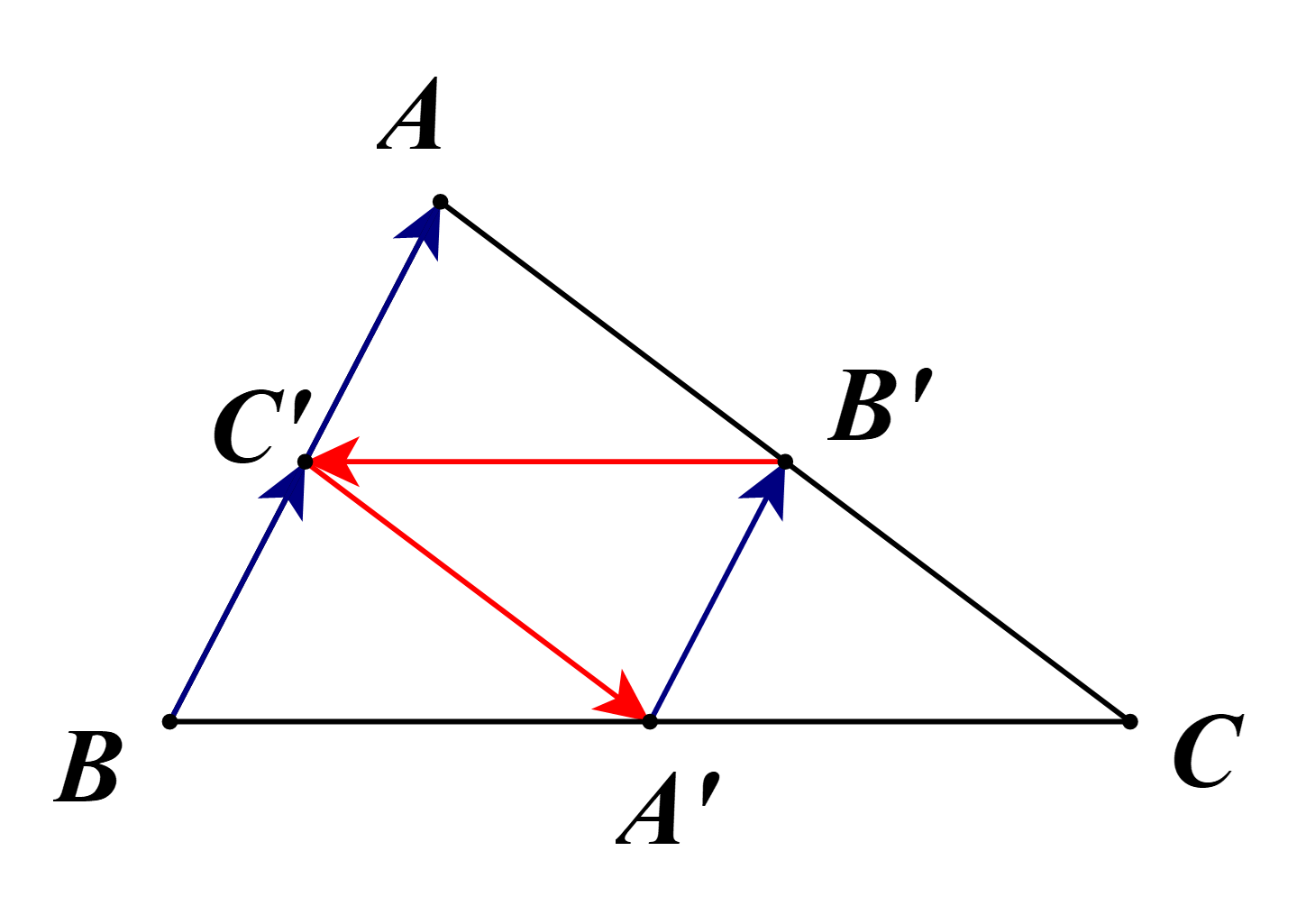
Tam giác ABC có A’B’ là đường trung bình.
Suy ra A’B’ = BC’ = C’A.
Mà \(\overrightarrow {BC'} ,\,\overrightarrow {C'A} ,\,\overrightarrow {A'B'} \) cùng phương với nhau.
Do đó \(\overrightarrow {BC'} = \overrightarrow {C'A} = \overrightarrow {A'B'} \).
Vì vậy phương án A đúng.
Tương tự như trên, ta có \(\overrightarrow {B'C'} = \overrightarrow {A'B} = \overrightarrow {CA'} \).
Do đó phương án B đúng.
Tam giác ABC có C’A’ là đường trung bình.
Suy ra \(C'A' = \frac{1}{2}AC\).
Mà \(\overrightarrow {C'A'} ,\,\overrightarrow {AC} \) cùng phương.
Do đó \(\overrightarrow {C'A'} = \frac{1}{2}\overrightarrow {AC} \).
Vì vậy phương án C đúng.
Vậy phương án D sai.

