Cho tam giác ABC có 3 góc nhọn và AB < AC. Các đường cao BE, CF cắt nhau
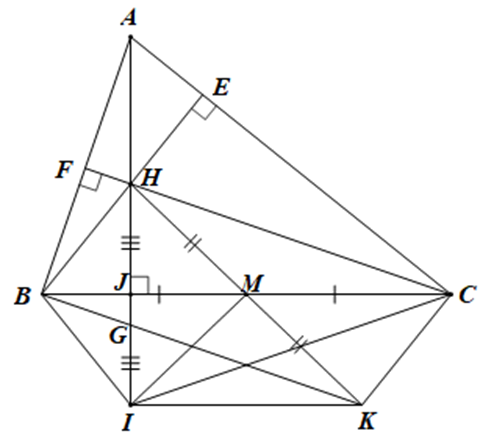
a) Xét tứ giác BHCK có:
MH = MK và MB = MI
Suy ra: BHCK là hình bình hành.
b) Vì BHCK là hình bình hành (chứng minh câu a)
Suy ra: BK // HC và CK // BH (tính chất hình bình hành)
Mà CH ⊥ AB và BH ⊥ AC
Suy ra: BK ⊥ AB và CK ⊥ AC.
c) Vì I đối xứng với H qua BC nên BC là đường trung trực của HI
Mà M thuộc BC, suy ra MH = MI (tính chất đường trung trực)
Mà \[MH = MK = \frac{1}{2}HK\]
Suy ra: \[MI = MH = MK = \frac{1}{2}HK\]
Do đó tam giác HIK vuông tại I hay HI ⊥ IK
Mà BC ⊥ HI (do BC là đường trung trực của HI)
Suy ra IK // BC
Do đó BIKC là hình thang (1)
Ta có BC là đường trung trực của HI, suy ra CI = CH
Mà CH = BK (vì BKCH là hình bình hành)
Suy ra BK = CI (2)
Từ (1) và (2) suy ra BICK là hình thang cân (dấu hiệu nhận biết)
d) Gọi giao điểm của BC và HI là J.
Vì BK // CH nên GHCK là hình thang
Để hình thang GHCK là hình thang cân thì \(\widehat {GHC} = \widehat {KCH}\)
Mà \(\widehat {HCK} + \widehat {HCA} = 90^\circ \) và \(\widehat {GHC} + \widehat {HCB} = 90^\circ \) (vì tam giác HJC vuông tại J)
Suy ra \(\widehat {HCA} = \widehat {HCB}\)
Do đó CH là đường phân giác của tam giác ABC
Lại có CH là đường cao của tam giác ABC
Suy ra tam giác ABC cân tại C
Vậy tam giác ABC cân tại C thì GHCK là hình thang cân.