Lời giải
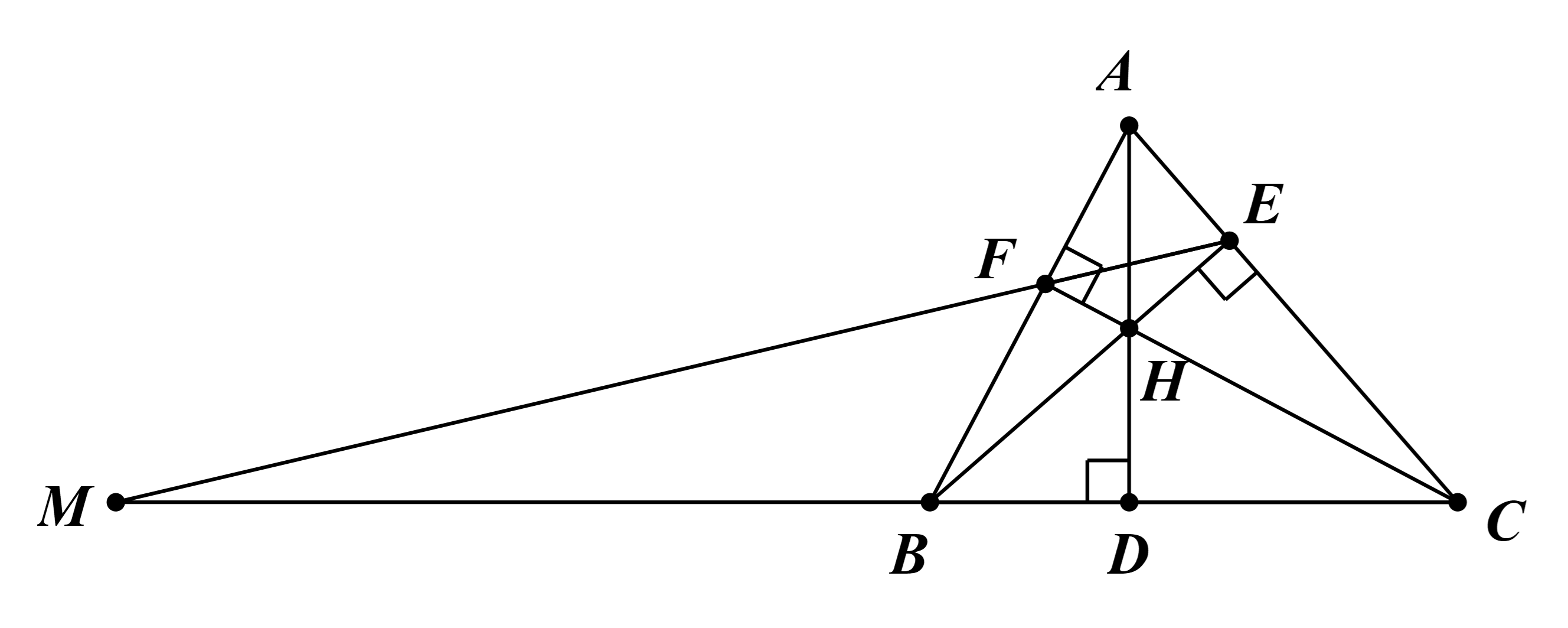
a) Xét ∆BAE và ∆CAF, có:
\(\widehat A\) chung;
\(\widehat {BEA} = \widehat {CFA} = 90^\circ \).
Do đó (g.g).
Suy ra \(\frac{{AB}}{{AC}} = \frac{{AE}}{{AF}}\).
Xét ∆AEF và ∆ABC, có:
\(\widehat A\) chung;
\(\frac{{AF}}{{AC}} = \frac{{AE}}{{AB}}\,\,\,\left( {do\,\,\frac{{AB}}{{AC}} = \frac{{AE}}{{AF}}} \right)\).
Do đó (c.g.c).
b) Ta có \(\widehat {AFE} = \widehat {ACB}\) (do ) và \(\widehat {AFE} = \widehat {MFB}\) (2 góc đối đỉnh).
Suy ra \(\widehat {MFB} = \widehat {ACB}\).
Xét ∆MFB và ∆MCE, có:
\(\widehat M\) chung;
\(\widehat {MFB} = \widehat {ACB}\) (chứng minh trên).
Do đó (g.g).
Suy ra \(\frac{{MF}}{{MC}} = \frac{{MB}}{{ME}}\).
Vậy ME.MF = MB.MC (điều phải chứng minh).
c) Ta có \({S_{ABC}} = 24 \Leftrightarrow \frac{1}{2}AD.BC = 24\)
⇔ AD.(BD + CD) = 48 ⇔ AD.(3 + 5) = 48.
⇔ AD = 6.
Ta có:
⦁ \(\widehat {HBD} + \widehat {BHD} = 90^\circ \) (do tam giác BHD vuông tại D);
⦁ \(\widehat {AHE} + \widehat {HAE} = 90^\circ \) (do tam giác AHE vuông tại E);
⦁ \(\widehat {BHD} = \widehat {AHE}\) (hai góc đối đỉnh).
Suy ra \(\widehat {HBD} = \widehat {HAE}\).
Xét ∆BHD và ∆ACD, có:
\(\widehat {BDH} = \widehat {ADC} = 90^\circ \);
\(\widehat {HBD} = \widehat {DAC}\) (chứng minh trên).
Do đó (g.g).
Suy ra \(\frac{{BD}}{{AD}} = \frac{{HD}}{{CD}}\).
Khi đó \(HD = \frac{{CD.BD}}{{AD}} = \frac{{5.3}}{6} = \frac{5}{2}\).
Vậy \({S_{BHC}} = \frac{1}{2}HD.BC = \frac{1}{2}.\frac{5}{2}.\left( {3 + 5} \right) = 10\).

