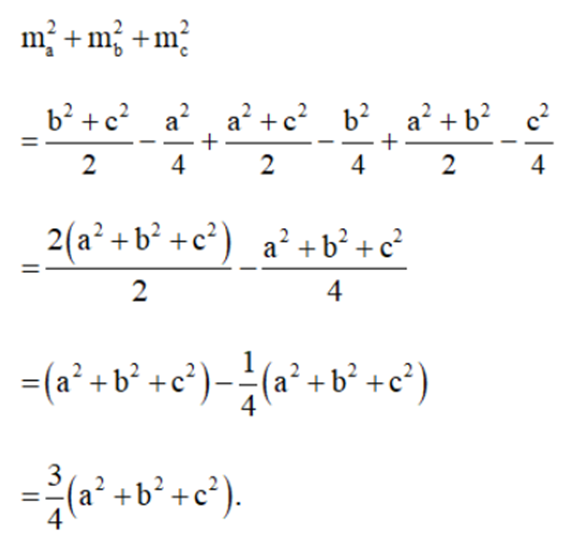Cho tam giác ABC. Chứng minh rằng:

a) \(\cot {\rm{A + cot B + cot C}} = \frac{{{a^2} + {b^2} + {c^2}}}{{4{\rm{S}}}}\).

b) \(m_a^2 + m_b^2 + m_c^2 = \frac{3}{4}\left( {{a^2} + {b^2} + {c^2}} \right)\).

a) Áp dụng định lí côsin ta có: cos A = \(\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)

Ta có \(S = \frac{1}{2}bc\sin A\), suy ra  \(\sin A = \frac{{2{\rm{S}}}}{{bc}}\)

Do đó cot A = \(\frac{{co{\rm{sA}}}}{{\sin {\rm{A}}}} = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}:\frac{{2{\rm{S}}}}{{bc}} = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}.\frac{{bc}}{{2{\rm{S}}}} = \frac{{{b^2} + {c^2} - {a^2}}}{{4{\rm{S}}}}\)

Chứng minh tương tự ta có:

\(\cot B = \frac{{{a^2} + {c^2} - {b^2}}}{{4{\rm{S}}}}\);  \(\cot C = \frac{{{a^2} + {b^2} - {c^2}}}{{4{\rm{S}}}}\)

Do đó:

\(\cot {\rm{A + cot B + cot C = }}\frac{{{c^2} + {b^2} - {a^2}}}{{4{\rm{S}}}} + \frac{{{a^2} + {c^2} - {b^2}}}{{4{\rm{S}}}} + \frac{{{a^2} + {b^2} - {c^2}}}{{4{\rm{S}}}} = \frac{{{a^2} + {b^2} + {c^2}}}{{4{\rm{S}}}}\)

Vậy \(\cot {\rm{A + cot B + cot C}} = \frac{{{a^2} + {b^2} + {c^2}}}{{4{\rm{S}}}}\).

b) Áp dụng công thức độ dài đường trung tuyến ta có:

\(m_a^2 = \frac{{{b^2} + {c^2}}}{2} - \frac{{{a^2}}}{4}\), \(m_b^2 = \frac{{{a^2} + {c^2}}}{2} - \frac{{{b^2}}}{4}\) và \(m_c^2 = \frac{{{a^2} + {b^2}}}{2} - \frac{{{c^2}}}{4}\)

Suy ra:

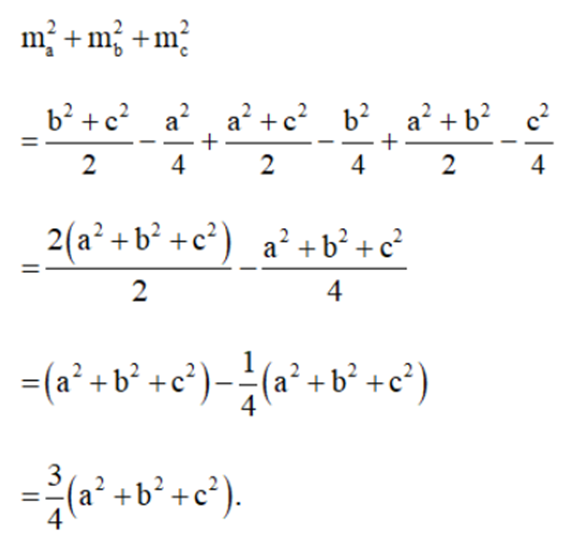
Vậy \(m_a^2 + m_b^2 + m_c^2 = \frac{3}{4}\left( {{a^2} + {b^2} + {c^2}} \right)\).