Cho tam giác ABC. Chứng minh: cotA + cotB + cotC

Đề bài: Cho tam giác ABC. Chứng minh: $\cot A+\cot B+\cot C=\frac{a^2+b^2+c^2}{4S}$.

Trả lời

Hướng dẫn giải:

Ta có:

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$

Mà:

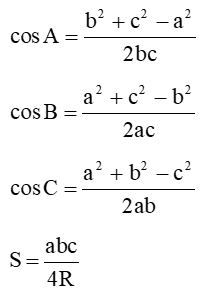
Từ đó, ta có:

$\begin{array}{l}\cot A+\cot B+\cot C\\ =\frac{\cos A}{\sin A}+\frac{\cos B}{\sin B}+\frac{\cos C}{\sin C}\\ =\frac{\frac{b^2+c^2-a^2}{2bc}}{\frac{a}{2R}}+\frac{\frac{a^2+c^2-b^2}{2ac}}{\frac{a}{2R}}+\frac{\frac{a^2+b^2-c^2}{2ab}}{\frac{a}{2R}}\\ =\frac{R}{abc}\left(b^2+c^2-a^2+c^2+a^2-b^2+a^2+b^2-c^2\right)\\ =\frac{a^2+b^2+c^2}{4S}\end{array}$