Cho tam giác ABC cân tại B. Hai trung tuyến AM, BN cắt nhau tại G. Gọi I và K lần lượt là trung điểm của GB, GC

Câu 3 trang 53 SBT Toán 8 Tập 1: Cho tam giác ABC cân tại B. Hai trung tuyến AM, BN cắt nhau tại G. Gọi I và K lần lượt là trung điểm của GB, GC. Khẳng định nào đúng?

A. $MN=\frac{1}{2}AC.$

B. $BC=\frac{1}{2}IK.$

C. MN > IK.

D. MN = IK.

Trả lời

Đáp án đúng là: D

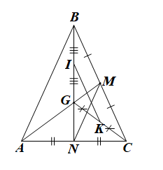
Trong ∆ABC có M là trung điểm của BC, N là trung điểm của AC nên MN là đường trung bình của ∆ABC

Suy ra $MN=\frac{1}{2}AB$ (tính chất đường trung bình trong tam giác). (1)

Trong ∆BGC có I là trung điểm của BG, K là trung điểm của BC nên IK là đường trung bình của ∆BGC

Suy ra $IK=\frac{1}{2}BC$ (tính chất đường trung bình trong tam giác). (2)

Mà tam giác ABC cân tại B nên BA = BC (3)

Từ (1), (2), (3) suy ra MN = IK.

Xem thêm các bài giải Toán lớp 8 sách Kết nối tri thức hay, chi tiết khác:

Bài 16: Đường trung bình của tam giác

Bài 17: Tính chất đường phân giác của tam giác

Bài tập cuối chương 4

Bài 18: Thu thập và phân loại dữ liệu

Bài 19: Biểu diễn dữ liệu bằng bảng, biểu đồ

Bài 20: Phân tích số liệu thống kê dựa vào biểu đồ