Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE

Bài 4.16 trang 55 SBT Toán 8 Tập 1: Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE, CD. Gọi I, K theo thứ tự là giao điểm của MN với BD và CE. Chứng minh MI = IK = KN.

Trả lời

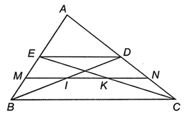
Trong ∆ABC có các đường trung tuyến BD, CE nên D là trung điểm của AC, E là trung điểm của AB nên ED là đường trung bình của ∆ABC

Suy ra $ED=\frac{1}{2}BC$ và ED // BC (tính chất đường trung bình của tam giác)

Ta có: E là trung điểm của AB nên $AE=EB=\frac{1}{2}AB$

Mà M là trung điểm của EB nên $EM=MB=\frac{1}{2}EB=\frac{1}{4}AB$ hay $\frac{MB}{AB}=\frac{1}{4}$

Tương tự, ta cũng có $NC=\frac{1}{4}AC$ hay $\frac{NC}{AC}=\frac{1}{4}$

Suy ra $\frac{MB}{AB}=\frac{NC}{AC}\left(=\frac{1}{4}\right)$

Xét DABC có $\frac{MB}{AB}=\frac{NC}{AC}$ nên MN // BC (định lí Thalès đảo)

Lại có ED // BC nên ED // MN // BC.

Xét DBDE có M là trung điểm của EB và MI // ED (do ED // MN)

Suy ra I là trung điểm của BD hay IB = ID

Khi đó MI là đường trung bình của DBDE nên $MI=\frac{1}{2}ED$.

Tương tự, trong DCDE ta cũng có $KN=\frac{1}{2}ED,$ trong DBCE có $MK=\frac{1}{2}BC$.

Ta có $IK=MK-MI=\frac{1}{2}BC-\frac{1}{2}ED=ED-\frac{1}{2}ED=\frac{1}{2}ED$.

Do đó $MI=IK=KN=\frac{1}{2}ED$.

Xem thêm các bài giải Toán lớp 8 sách Kết nối tri thức hay, chi tiết khác:

Bài 16: Đường trung bình của tam giác

Bài 17: Tính chất đường phân giác của tam giác

Bài tập cuối chương 4

Bài 18: Thu thập và phân loại dữ liệu

Bài 19: Biểu diễn dữ liệu bằng bảng, biểu đồ

Bài 20: Phân tích số liệu thống kê dựa vào biểu đồ