Giải SBT Toán 8 (Kết nối tri thức) Bài 17: Tính chất đường phân giác của tam giác

Giải SBT Toán 8 (Kết nối tri thức) Bài 17: Tính chất đường phân giác của tam giác

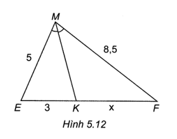
Bài 4.11 trang 52 SBT Toán 8 Tập 1: Tìm độ dài x trong Hình 5.12.

Lời giải:

Trong ∆MEF có MK là phân giác của góc M nên ta có $\frac{KE}{KF}=\frac{ME}{MF}$(tính chất đường phân giác của tam giác)

Hay $\frac{3}{KF}=\frac{5}{\mathrm{8,5}}$, suy ra $KF=\frac{3\cdot \mathrm{8,5}}{5}=\mathrm{5,1}$.

Vậy x = 5,1.

Bài 4.12 trang 52 SBT Toán 8 Tập 1: Cho tam giác ABC, trung tuyến AI. Tia phân giác góc AIB và tia phân giác góc AIC cắt AB, AC lần lượt tại M và N. Chứng minh MN // BC.

Lời giải:

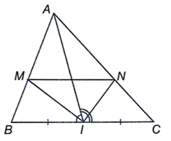
Trong ∆AIB, IM là phân giác của $\widehat{AIB}$ nên $\frac{MA}{MB}=\frac{IA}{IB}$(tính chất đường phân giác của tam giác) (1)

Trong DAIC, IN là phân giác của $\widehat{AIC}$ nên $\frac{NA}{NC}=\frac{IA}{IC}$ (tính chất đường phân giác của tam giác) (2)

AI là đường trung tuyến của ∆ABC nên I là trung điểm của BC, do đó IB = IC (3)

Từ (1), (2), (3) ta có:$\frac{MA}{MB}=\frac{NA}{NC}$

Suy ra MN // BC (định lí Thales đảo).

Bài 4.13 trang 52 SBT Toán 8 Tập 1: Cho ∆ABC có AD, BE, CF lần lượt là đường phân giác của góc A, góc B, góc C (D ∈ BC, E ∈ AC, F ∈ AB). Chứng minh rằng: $\frac{AE}{EC}\cdot \frac{CD}{DB}\cdot \frac{BF}{FA}=1.$

Lời giải:

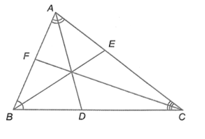
Trong ∆ABC có AD là phân giác của $\widehat{BAC}$ nên $\frac{DC}{DB}=\frac{AC}{AB}$ (tính chất đường phân giác của tam giác).

Tương tự, ta có BE, CF lần lượt là tia phân giác của $\widehat{B},\widehat{C}$.

Suy ra $\frac{EA}{EC}=\frac{BA}{BC};\frac{FB}{FA}=\frac{CB}{CA}$.

Do đó: $\frac{AE}{EC}\cdot \frac{CD}{DB}\cdot \frac{BF}{FA}=\frac{BA}{BC}\cdot \frac{AC}{AB}\cdot \frac{CB}{CA}=1$

Bài 4.14 trang 52 SBT Toán 8 Tập 1: Cho tam giác ABC, phân giác AD (D ∈ BC). Kẻ DE // AB (E ∈ AC). Chứng minh rằng: AB.EC = AC.EA.

Lời giải:

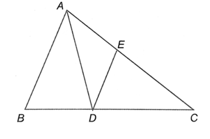
Trong ∆ABC có AD là phân giác của $\widehat{BAC}$ nên $\frac{DB}{DC}=\frac{AB}{AC}$ (tính chất đường phân giác của tam giác).

Trong ∆ADC có DE // AB nên $\frac{DB}{DC}=\frac{EA}{EC}$ (định lí Thalès trong tam giác).

Suy ra $\frac{AB}{AC}=\frac{EA}{EC}$ nên AB.EC = AC.EA.

Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác: 

Bài 15: Định lí Thalès trong tam giác

Bài 16: Đường trung bình của tam giác

Bài tập cuối chương 4

Bài 18: Thu thập và phân loại dữ liệu

Bài 19: Biểu diễn dữ liệu bằng bảng, biểu đồ