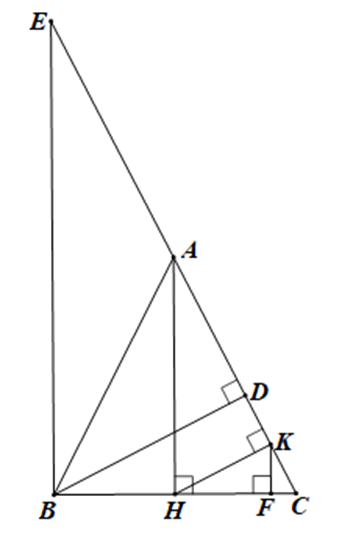
a) Xét tam giác AHC vuông ở H ta có

AC² = AH² + HC² (định lí Pytago)

Hay 25² = 20² + HC²

Suy ra HC = 15 (cm).

Xét tam giác AHC vuông ở H có HK ⊥ AC

Suy ra \(\frac{1}{{H{K^2}}} = \frac{1}{{A{H^2}}} + \frac{1}{{H{C^2}}}\) (hệ thức lượng trong tam giác vuông)

Hay \(\frac{1}{{H{K^2}}} = \frac{1}{{{{20}^2}}} + \frac{1}{{{{15}^2}}}\)

Suy ra HK = 12

Xét tam giác AHC có \(\sin C = \frac{{AH}}{{AC}} = \frac{{20}}{{25}}\)

Suy ra \(\widehat C \approx 53^\circ \)

b) Ta có BE // AH, AH ⊥ BC

Suy ra BE ⊥ BC

Hay tam giác BCE vuông tại B có BD ⊥ AC (giả thiết)

Suy ra BC² = CD . CE (hệ thức lượng trong tam giác vuông)

⟺ (2BH)² = CD . CE

⟺ 4BH² = CD . CE

⟺ \(B{H^2} = \frac{{C{\rm{D}}.CE}}{4}\)

c) Kẻ AT // BD (T ∈ BE)

Mà BD ⊥ AC suy ra AT ⊥ AC, hay \(\widehat {E{\rm{A}}T} = 90^\circ \).

Xét tứ giác ATB có AT // BO, BT // AO

Suy ra ATBO là hình bình hành

Do đó AT = BO (tính chất hình bình hành)

Vì AH // BE nên \(\widehat {CAH} = \widehat {AEB}\) (hai góc đồng vị)

Xét DEAT và DOAD có

\(\widehat {CAH} = \widehat {AEB}\) (cmt);

\(\widehat {E{\rm{A}}T} = \widehat {{\rm{ADO}}} = 90^\circ \)

Suy ra  (g.g)

Do đó \(\frac{{AT}}{{{\rm{DO}}}} = \frac{{{\rm{EA}}}}{{A{\rm{D}}}}\) (tỉ số đồng dạng)

Mà AT = BO (chứng minh trên)

Suy ra \(\frac{{OB}}{{O{\rm{D}}}} = \frac{{A{\rm{E}}}}{{A{\rm{D}}}}\).

d) Xét tam giác KFC có CF = CK . sin \(\widehat {CKF}\)

Xét tam giác KHC có CK = HC . sin \(\widehat {KHC}\)

Xét tam giác AHC có HC = AC . sin \(\widehat {HAC}\)

Suy ra \(CF = AC.\sin \widehat {HAC}.\sin \widehat {KHC}.\sin \widehat {CKF}\)

Mà \(\widehat {HAC} = \widehat E\) (hai góc đồng vị);

      \(\widehat {KHC} = \widehat E\) (cùng phụ với góc \(\widehat C\));

      \(\widehat {CKF} = \widehat E\) (cùng phụ với góc \(\widehat C\))

Do đó CF = AC. sin³E

Vậy CF = AC. sin³E.