Cho tam giác ABC cân tại A đường cao AH và BK cắt nhau tại I

Đề bài: Cho tam giác ABC cân tại A đường cao AH và BK cắt nhau tại I. Chứng minh:

a) Đường tròn đường kính AI đi qua K.

b) HK là tiếp tuyến của đường tròn đường kính AI.

Trả lời

Hướng dẫn giải:

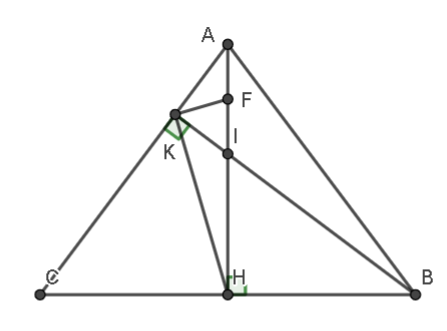
a)

Gọi F là trung điểm của AI

Do BK là đường cao của tam giác ABC nên $\widehat{BKA}=90°$

Xét tam giác AKI vuông tại K có:

KF là đường trung tuyến ứng với cạnh huyền.

Do đó, KF = FI = FA

Vậy K nằm trên đường tròn đường kính AI.

b)

Xét tam giác AKF có: FA =FK (cmt)

Do đó, AKF cân tại F

$\Rightarrow \widehat{FAK}=\widehat{FKA}$ (1)

Do AH là đường cao của tam giác ABC cân tại A nên ta AH cũng là đường trung tuyến hay H là trung điểm của BC

Xét tam giác CKB vuông tại K có:

KH là đường trung tuyến ứng với cạnh huyền

⇒ KH = CH = BH

Xét tam giác CHK có: CH = HK (cmt)

Do đó, tam giác CHK cân tại H  $\Rightarrow \widehat{HCK}=\widehat{HKC}$ (2)

Xét tam giác AHC vuông tại H có: $\widehat{FAK}+\widehat{HCK}=90°$ (3)

Từ (1), (2) và (3) ta có: $\widehat{FKA}+\widehat{HKC}=90°$

$\Rightarrow \widehat{FKH}=90°$

Do đó, HK vuông góc với FK mà FK là bán kính của đường tròn đường kính AI.

Vậy HK là tiếp tuyến của đường tròn đường kính AI.