Cho tam giác ABC cân tại A, đường cao AD, trực tâm H. Tính độ dài AD biết AH = 14 cm, BH = HC = 30 cm
Câu 28: Cho tam giác ABC cân tại A, đường cao AD, trực tâm H. Tính độ dài AD biết AH = 14 cm, BH = HC = 30 cm.
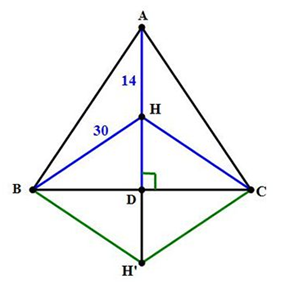
Gọi H’ là điểm đối xứng H qua BC.
Suy ra D là trung điểm của HH’
Vì tam giác ABC cân tại A, AD là đường cao nên AD là trung tuyến
Suy ra D là trung điểm của BC
Xét tứ giác BHCH’ có
D là trung điểm của HH’ và BC;
BC và HH’ là hai đường chéo
Suy ra BHCH’ là hình bình hành.
Mà BH = CH nên hình bình hành BHCH’ là hình thoi
Do đó BH’ // CH, BH = BH’.
Lại có CH ⊥ AB (vì H là trực tâm của tam giác ABC) nên BH’⊥ AB
Hay tam giác ABH’ vuông tại B
Mà BD ⊥ AH’
Suy ra H’B2 = H’D . H’A
⇔ HB2 = HD . (2HD + HA)
⇔ 302 = HD . (2HD + 14)
⇔ 2HD2 + 14HD – 900 = 0
⇔ (HD + 25)(HD – 18) = 0
⇔ HD – 18 = 0 (vì HD > 0)
⇔ HD = 18
Ta có AD = AH + HD = 14 + 18 = 32 cm
Vậy AD = 32 cm.