Bài 66 trang 88 SBT Toán 7 Tập 2: Cho tam giác ABC cân tại A có M là trung điểm BC; ME vuông góc với AB tại E, MF vuông góc với AC tại F. Chứng minh:
a) AM là trung trực của đoạn thẳng BC;
b) ME = MF và AM là đường trung trực của đoạn thẳng EF.
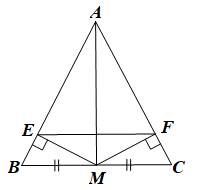
a) Tam giác ABC cân tại A nên AB = AC (hai cạnh bên).
Suy ra A thuộc đường trung trực của BC.
Lại có M là trung điểm của BC.
Nên AM là đường trung trực của BC.
Vậy AM là trung trực của đoạn thẳng BC.
b) Vì tam giác ABC cân tại A nên (hai góc ở đáy).
Xét EBM và FCM có:
,
BM = CM (do M là trung điểm của BC),
(chứng minh trên)
Do đó ∆EBM = ∆FCM (cạnh huyền – góc nhọn).
Suy ra ME = MF, BE = CF (các cặp cạnh tương ứng).
Do đó M thuộc đường trung trực của EF (1)
Ta có AB = AE + EB, AC = AF + FC.
Mà AB = AC, BE = CF nên AE = AF.
Suy ra A thuộc đường trung trực của EF (2)
Từ (1) và (2) suy ra AM là đường trung trực của EF.
Vậy ME = MF và AM là đường trung trực của EF.
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 8. Đường vuông góc và đường xiên
Bài 9. Đường trung trực của một đoạn thẳng
Bài 10. Tính chất ba đường trung tuyến của tam giác