Cho tam giác ABC cân ở A và H là trung điểm BC.Gọi I là hình chiếu vuông góc của H lên AC và O là trung điểm của HI. Chứng minh
a) \(\widehat {AHO} = \widehat {BCI}\)
b) AH . IC = HI . HC = HO . BC
c) Tam giác AHO đồng dạng tam giác BCI
d) AO vuông góc BI.
Lời giải
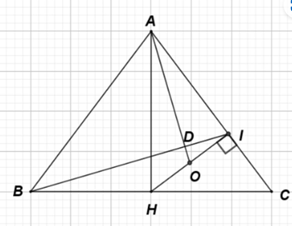
a) Vì tam giác ABC cân tại A nên AB = AC
Vì H là trung điểm của BC nên HA = HC
Xét tam giác AHB và tam giác AHC có
AH là cạnh chung
AB = AC (chứng minh trên)
HA = HC (chứng minh trên)
Do đó ΔAHB = ΔAHC (c.c.c)
Suy ra \(\widehat {AHB} = \widehat {AHC}\) (hai góc tương ứng)
Mà \(\widehat {AHB} + \widehat {AHC} = 180^\circ \)
Suy ra \(\widehat {AHB} = \widehat {AHC} = 90^\circ \)
Hay AH ⊥ BC
Vì tam giác HIC vuông tại I nên \(\widehat {IHC} + \widehat {ICH} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Mà \(\widehat {AHO} + \widehat {IHC} = \widehat {AHC} = 90^\circ \)
Suy ra \(\widehat {AHO} = \widehat {BCI}\)
Vậy \(\widehat {AHO} = \widehat {BCI}\).
b) Xét ΔAHI và ΔHCI có:
\(\widehat {AHI} = \widehat {HCI}\) (chứng minh câu a)
\(\widehat {AIH} = \widehat {CIH}\left( { = 90^\circ } \right)\)
Do đó (g.g)
Suy ra AH . IC = HI . HC
Mà HI = 2. HO; HC = \(\frac{{{\rm{BC}}}}{2}\)
Suy ra HI . HC = 2 . HO . \(\frac{{{\rm{BC}}}}{2}\) = HO . BC
Vậy AH . IC = HI . HC = HO . BC
c) Vì AH . IC = HO . BC nên \(\frac{{AH}}{{HO}} = \frac{{BC}}{{IC}}\)
Xét ΔAHO và ΔBCI có:
\(\frac{{AH}}{{HO}} = \frac{{BC}}{{IC}}\) (chứng minh trên)
\(\widehat {AHO} = \widehat {BCI}\) (chứng minh câu a)
Suy ra (c.g.c)
d) Vì nên \(\widehat {HAO} = \widehat {CBI}\)
Gọi giao điểm của AO và BI là D
Xét tam giác ABD có \(\widehat {AB{\rm{D}}} + \widehat {A{\rm{D}}B} + \widehat {DAB} = 180^\circ \) (tổng ba góc trong một tam giác)
Hay \(\widehat {AB{\rm{D}}} + \widehat {DAH} + \widehat {BAH} + \widehat {A{\rm{D}}B} = 180^\circ \)
Mà \(\widehat {HAD} = \widehat {CBI}\)
Suy ra \(\widehat {AB{\rm{D}}} + \widehat {CBI} + \widehat {BAH} + \widehat {A{\rm{D}}B} = 180^\circ \)
Nên \(\widehat {ABH} + \widehat {BAH} + \widehat {A{\rm{D}}B} = 180^\circ \)
Lại có \(\widehat {ABH} + \widehat {BAH} = 90^\circ \) (vì tam giác AHB vuông tại H)
Suy ra \(\widehat {A{\rm{D}}B} = 90^\circ \)
Nên AO ⊥ BI
Vậy AO ⊥ BI.