Cho tam giác ABC cân ở A. Gọi I là giao điểm các đường phân giác. a) Xác định vị trí tương đối của đường thẳng AC với đường tròn (O) ngoại tiếp ∆BIC b) Gọi H là trung điểm của BC. Kẻ đường
30
19/05/2024
Cho tam giác ABC cân ở A. Gọi I là giao điểm các đường phân giác.
a) Xác định vị trí tương đối của đường thẳng AC với đường tròn (O) ngoại tiếp ∆BIC
b) Gọi H là trung điểm của BC. Kẻ đường kính IK của đường tròn (O).
Chứng minh: \(\frac{{AI}}{{AK}} = \frac{{HI}}{{HK}}\).
Trả lời
Lời giải
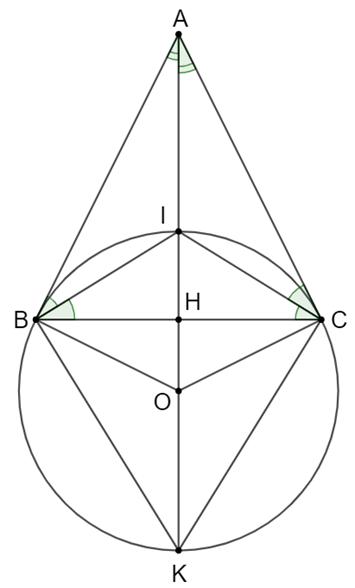
a) Vì tam giác ABC cân ở A Þ AI vừa là đường phân giác vừa là đường cao.
Do 3 điểm A, I, O thẳng hàng Þ AO ^ BC
Þ \(\widehat {OIC} + \widehat {ICB} = 90^\circ \) (1)
Vì OI = OC = R Þ ∆IOC cân tại O
Þ \(\widehat {OIC} = \widehat {ICO}\) (2)
Do CI là đường phân giác của \(\widehat C\) nên suy ra \(\widehat {ICB} = \widehat {ICA}\) (3)
Từ (1), (2) và (3) suy ra \(\widehat {ICA} + \widehat {ICO} = 90^\circ \)
\( \Rightarrow \widehat {ACO} = 90^\circ \Rightarrow AC \bot CO\)
Vậy AC là tiếp tuyến của đường tròn tâm O.
b) Do ∆CIK nội tiếp đường tròn (O)
\( \Rightarrow \widehat {ICK} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Þ CK ^ CI
Mà CI là đường phân giác góc trong \(\widehat C\)
Þ CK là đường phân giác góc ngoài của \(\widehat {ACB}\)
Nên theo tích chất đường phân giác ta có:
\(\frac{{AI}}{{AK}} = \frac{{HI}}{{HK}}\) (đpcm).

