Cho tam giác ABC (AB > AC) có đường cao AH . Gọi M , N, P lần lượt là trung
Cho tam giác ABC (AB > AC) có đường cao AH . Gọi M , N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh: MNPH là hình thang cân.
Cho tam giác ABC (AB > AC) có đường cao AH . Gọi M , N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh: MNPH là hình thang cân.
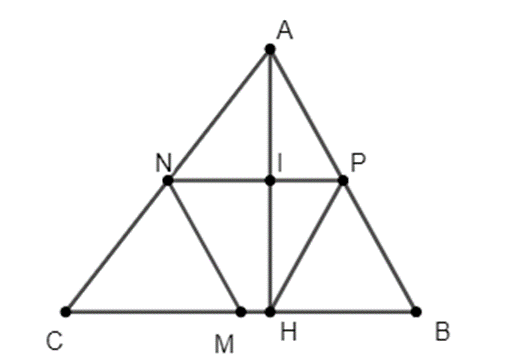
Ta có:
N là trung điểm của AC;
P là trung điểm của AB.
Suy ra NP là đường trung bình của ∆ABC.
Suy ra MP // BC
Suy ra MNPH là hình thang (1).
Ta có:
\(\widehat B = \widehat {NMC}\) (đồng vị, AB // MN)
\(\widehat B = \widehat {PHB}\) (\(\Delta PHB\) cân)
Suy ra \(\widehat {NMC} = \widehat {PHB}\) \( \Rightarrow \widehat {NMH} = \widehat {PHM}\)(2)
Từ (1) và (2) suy ra được tứ giác MNPH là hình thang cân.